
【題目】隨著社會發展,淮北市在一天的上下班時段也出現了堵車嚴重的現象。交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念.記交通指數為T,其范圍為[0,10],分別有5個級別:T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10]嚴重擁堵.早高峰時段(T≥3 ),從淮北市交通指揮中心隨機選取了一至四馬路之間50個交通路段,依據交通指數數據繪制的直方圖如圖所示:
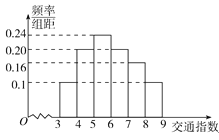
(I)據此直方圖估算交通指數T∈[4,8)時的中位數和平均數;
(II)據此直方圖求出早高峰一至四馬路之間的3個路段至少有2個嚴重擁堵的概率是多少?
(III)某人上班路上所用時間若暢通時為20分鐘,基本暢通為30分鐘,輕度擁堵為35分鐘,中度擁堵為45分鐘,嚴重擁堵為60分鐘,求此人用時間的數學期望.
【答案】(1)4.72.(2)![]() (3)40.6
(3)40.6
【解析】試題分析:(1)由直方圖可得,根據中位數的計算公式可求得中位數,利用頻率直方圖,可計算交通指數的平均數。
(2)設事件![]() 為“1條路段嚴重擁堵”,得
為“1條路段嚴重擁堵”,得![]() ,則
,則![]() 條路段中至少有
條路段中至少有![]() 條路段嚴重擁堵的概率。
條路段嚴重擁堵的概率。
(3)由題意,得到時間X的分布列,利用期望的公式,即可求解數學期望,得到結論。
試題解析:
(1)由直方圖知:T∈[4,8)時交通指數的中位數在T∈[5,6),且為 5+1×![]() =
=![]()
T∈[4,8)時交通指數的平均數為:
4.5×0.2+5.5×0.24+6.5×0.2+7.5×0.16=4.72.
(2)設事件A為“1條路段嚴重擁堵”,則P(A)=0.1,
則3條路段中至少有2條路段嚴重擁堵的概率為:
P=C32×(![]() )2×(1-
)2×(1-![]() )+C33×(
)+C33×(![]() )3=
)3=![]() ,
,
所以3條路段中至少有2條路段嚴重擁堵的概率為![]() .
.
(3)由題意,所用時間X的分布列如下表:
X | 30 | 35 | 45 | 60 |
P | 0.1 | 0.44 | 0.36 | 0.1 |
則E(X)=30×0.1+35×0.44+45×0.36+60×0.1=40.6,
所以此人上班路上所用時間的數學期望是40.6分鐘.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() (
(![]() 為常數).
為常數).
(1)函數![]() 的圖象在點
的圖象在點![]() 處的切線與函數
處的切線與函數![]() 的圖象相切,求實數
的圖象相切,求實數![]() 的值;
的值;
(2)若函數![]() 在定義域上存在單調減區間,求實數
在定義域上存在單調減區間,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,
, ![]() ,且
,且![]() ,都有
,都有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,D,E分別為△ABC邊AB,AC的中點,直線DE交△ABC的外接圓于F,G兩點,若CF∥AB,證明: 
(1)CD=BC;
(2)△BCD∽△GBD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學組織了一次高二文科學生數學學業水平模擬測試,學校從測試合格的男、女生中各隨機抽取100人的成績進行統計分析,分別制成了如圖所示的男生和女生數學成績的頻率分布直方圖.

(Ⅰ)若所得分數大于等于80分認定為優秀,求男、女生優秀人數各有多少人?
(Ⅱ)在(Ⅰ)中的優秀學生中用分層抽樣的方法抽取5人,從這5人中任意任取2人,求至少有一名男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在某港口![]() 處獲悉,其正東方向距離20n mile的
處獲悉,其正東方向距離20n mile的![]() 處有一艘漁船遇險等待營救,此時救援船在港口的南偏西30°距港口10n mile的C處,救援船接到救援命令立即從C處沿直線前往B處營救漁船.
處有一艘漁船遇險等待營救,此時救援船在港口的南偏西30°距港口10n mile的C處,救援船接到救援命令立即從C處沿直線前往B處營救漁船.
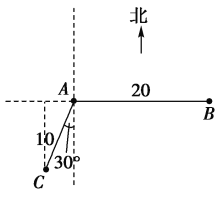
(1)求接到救援命令時救援船距漁船的距離;
(2)試問救援船在C處應朝北偏東多少度的方向沿直線前往B處救援?(已知![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 的底面是邊長為2的正三角形且側棱垂直于底面,側棱長是
的底面是邊長為2的正三角形且側棱垂直于底面,側棱長是![]() ,
, ![]() 是
是![]() 的中點.
的中點.
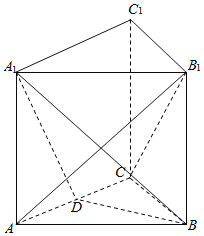
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com