
已知函數![]() =
=![]() +
+![]() 有如下性質:如果常數
有如下性質:如果常數![]() >0,那么該函數在
>0,那么該函數在![]() 0,
0,![]()
![]() 上是減函數,在
上是減函數,在![]()
![]() ,+∞
,+∞![]() 上是增函數.
上是增函數.
(1)如果函數![]() =
=![]() +
+![]() (
(![]() >0)的值域為
>0)的值域為![]() 6,+∞
6,+∞![]() ,求
,求![]() 的值;
的值;
(2)研究函數![]() =
=![]() +
+![]() (常數
(常數![]() >0)在定義域內的單調性,并說明理由;
>0)在定義域內的單調性,并說明理由;
(3)對函數![]() =
=![]() +
+![]() 和
和![]() =
=![]() +
+![]() (常數
(常數![]() >0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
>0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數![]() =
=![]() +
+![]() (
(![]() 是正整數)在區間[
是正整數)在區間[![]() ,2]上的最大值和最小值(可利用你的研究結論).
,2]上的最大值和最小值(可利用你的研究結論).
解(1) 函數y=x+![]() (x>0)的最小值是2
(x>0)的最小值是2![]() ,則2
,則2![]() =6, ∴b=log29.
=6, ∴b=log29.
(2)設0< x1< x2, y2-y1=![]() .
.
當![]() <x1<x2時, y2>y1, 函數y=
<x1<x2時, y2>y1, 函數y=![]() 在[
在[![]() ,+∞)上是增函數;
,+∞)上是增函數;
當0< x1< x2<![]() 時y2< y1, 函數y=
時y2< y1, 函數y=![]() 在(0,
在(0,![]() ]上是減函數.
]上是減函數.
又y=![]() 是偶函數,于是,該函數在(-∞,-
是偶函數,于是,該函數在(-∞,-![]() ]上是減函數, 在[-
]上是減函數, 在[-![]() ,0)上是增函數.
,0)上是增函數.
(3)可以把函數推廣為 y=![]() (常數a>0),其中n是正整數.
(常數a>0),其中n是正整數.
當n是奇數時,函數y=![]() 在(0,
在(0,![]() ]上是減函數,在[
]上是減函數,在[![]() ,+∞) 上是增函數,
,+∞) 上是增函數,
在(-∞,-![]() ]上是增函數, 在[-
]上是增函數, 在[-![]() ,0)上是減函數.
,0)上是減函數.
當n是偶數時,函數y=![]() 在(0,
在(0,![]() ]上是減函數,在[
]上是減函數,在[![]() ,+∞) 上是增函數,
,+∞) 上是增函數,
在(-∞,-![]() ]上是減函數, 在[-
]上是減函數, 在[-![]() ,0)上是增函數.
,0)上是增函數.
F(x)= ![]() +
+![]()
=![]()
因此F(x) 在 [![]() ,1]上是減函數,在[1,2]上是增函數.
,1]上是減函數,在[1,2]上是增函數.
所以,當x=![]() 或x=2時, F(x)取得最大值(
或x=2時, F(x)取得最大值(![]() )n+(
)n+(![]() )n;
)n;
當x=1時F(x)取得最小值2n+1.


科目:高中數學 來源: 題型:
(06年上海卷理)(18分)
已知函數![]() =
=![]() +
+![]() 有如下性質:如果常數
有如下性質:如果常數![]() >0,那么該函數在
>0,那么該函數在![]() 0,
0,![]()
![]() 上是減函數,在
上是減函數,在![]()
![]() ,+∞
,+∞![]() 上是增函數.
上是增函數.
(1)如果函數![]() =
=![]() +
+![]() (
(![]() >0)的值域為
>0)的值域為![]() 6,+∞
6,+∞![]() ,求
,求![]() 的值;
的值;
(2)研究函數![]() =
=![]() +
+![]() (常數
(常數![]() >0)在定義域內的單調性,并說明理由;
>0)在定義域內的單調性,并說明理由;
(3)對函數![]() =
=![]() +
+![]() 和
和![]() =
=![]() +
+![]() (常數
(常數![]() >0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
>0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數![]() =
=![]() +
+![]() (
(![]() 是正整數)在區間[
是正整數)在區間[![]() ,2]上的最大值和最小值(可利用你的研究結論).
,2]上的最大值和最小值(可利用你的研究結論).
查看答案和解析>>
科目:高中數學 來源:2013屆內蒙古赤峰市高二下學期期末考試文科數學試卷(解析版) 題型:解答題
已知函數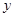 =
=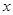 +
+ 有如下性質:如果常數
有如下性質:如果常數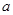 >0,那么該函數在
>0,那么該函數在 0,
0,
 上是減函數,在
上是減函數,在
 ,+∞
,+∞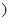 上是增函數.
上是增函數.
(Ⅰ)如果函數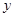 =
=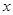 +
+ (
(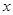 >0)的值域為
>0)的值域為 6,+∞
6,+∞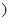 ,求
,求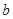 的值;
的值;
(Ⅱ)研究函數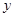 =
=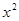 +
+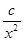 (常數
(常數 >0)在定義域內的單調性,并說明理由;
>0)在定義域內的單調性,并說明理由;
(Ⅲ)對函數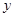 =
=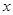 +
+ 和
和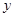 =
=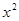 +
+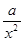 (常數
(常數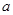 >0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
>0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數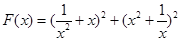 (
(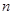 是正整數)在區間[
是正整數)在區間[ ,2]上的最大值和最小值(可利用你的研究結論).
,2]上的最大值和最小值(可利用你的研究結論).
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三數學10月單元練習(函數二) 題型:解答題
(本小題滿分14分)已知函數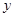 =
=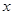 +
+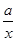 有如下性質:如果常數
有如下性質:如果常數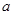 >0,那么該
>0,那么該
函數在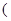 0,
0,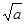
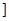 上是減函數,在
上是減函數,在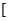
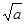 ,+∞
,+∞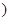 上是增函數.
上是增函數.
(1)如果函數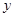 =
=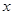 +
+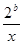 (
(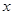 >0)的值域為
>0)的值域為 6,+∞
6,+∞ ,求
,求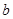 的值;
的值;
(2)研究函數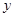 =
=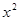 +
+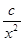 (常數
(常數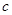 >0)在定義域內的單調性,并說明理由;
>0)在定義域內的單調性,并說明理由;
(3)對函數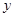 =
=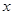 +
+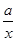 和
和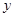 =
=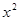 +
+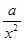 (常數
(常數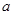 >0)作出推廣,使它們都是你所推廣的
>0)作出推廣,使它們都是你所推廣的
函數的特例.
(4)(理科生做)研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數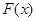 =
=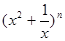 +
+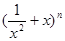 (
(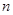 是正整數)在區間[
是正整數)在區間[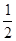 ,2]上的最大值和最小值(可利用你
,2]上的最大值和最小值(可利用你
的研究結論).
查看答案和解析>>
科目:高中數學 來源: 題型:
22.已知函數![]() =
=![]() +
+![]() 有如下性質:如果常數
有如下性質:如果常數![]() >0,那么該函數在
>0,那么該函數在![]() 0,
0,![]()
![]() 上是減函數,
上是減函數,
在![]()
![]() ,+∞
,+∞![]() 上是增函數.
上是增函數.
(1)如果函數![]() =
=![]() +
+![]() (
(![]() >0)的值域為
>0)的值域為![]() 6,+∞
6,+∞![]() ,求
,求![]() 的值;
的值;
(2)研究函數![]() =
=![]() +
+![]() (常數
(常數![]() >0)在定義域內的單調性,并說明理由;
>0)在定義域內的單調性,并說明理由;
(3)對函數![]() =
=![]() +
+![]() 和
和![]() =
=![]() +
+![]() (常數
(常數![]() >0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
>0)作出推廣,使它們都是你所推廣的函數的特例.研究推廣后的函數的單調性(只須寫出結論,不必證明),并求函數
![]() =
=![]() +
+![]() (
(![]() 是正整數)在區間[
是正整數)在區間[![]() ,2]上的最大值和最小值(可利用你的研究結論).
,2]上的最大值和最小值(可利用你的研究結論).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com