
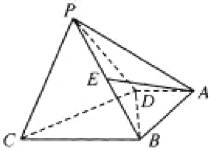
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() 和
和![]() 均為等邊三角形,且平面
均為等邊三角形,且平面![]() 平面
平面![]() ,點
,點![]() 為
為![]() 中點.
中點.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 的面積為
的面積為![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析;(2)![]() .
.
【解析】分析:(Ⅰ)證明線面平行,需在平面內構造一條線平行于已知直線,將直線![]() 沿
沿![]() 平移,點
平移,點![]() 至點
至點![]() 處,則點
處,則點![]() 應移至
應移至![]() 中點處,故取
中點處,故取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() .
.
若證![]() ,則需證明
,則需證明![]() 、
、![]() 平行且相等,
平行且相等,![]() 、
、![]() 需要以
需要以![]() 作為中間量.
作為中間量.
(Ⅱ)根據兩個等邊三角形和面面垂直,假設一邊長為x,表示![]() 的面積,解出x,求出三棱錐底面
的面積,解出x,求出三棱錐底面![]() 的面積.
的面積.
因為![]() 為
為![]() 中點,所以三棱錐
中點,所以三棱錐![]() 底面上的高為
底面上的高為![]() 到底面距離的一半.
到底面距離的一半.![]()
詳解:(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ;取
;取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
因為![]() 是正三角形,所以
是正三角形,所以![]() .
.
因為![]() ,所以四邊形
,所以四邊形![]() 為矩形,
為矩形,
從而![]() ,
,![]() .
.
因為![]() 為
為![]() 的中位線,
的中位線,
所以![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
所以四邊形![]() 是平行四邊形,從而
是平行四邊形,從而![]() ,
,
又![]() 面
面![]() ,所以
,所以![]() 面
面![]() .
.

(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() .
.
過點![]() 作
作![]() 交
交![]() 于
于![]() .
.
因為![]() ,面
,面![]() 面
面![]() ,面
,面![]() 面
面![]()
所以![]() 面
面![]() .又因為
.又因為![]() 面
面![]() ,所以
,所以![]() .
.
又因為![]() ,
,![]() ,
,![]() 面
面![]() ,.
,.
所以![]() 面
面![]() ,又因為
,又因為![]() 面
面![]() ,所以
,所以![]() .
.
由于![]() 為
為![]() 中點,易知
中點,易知![]() .
.
設![]() ,則
,則![]() 的面積為
的面積為![]() ,
,
解得![]() ,從而
,從而![]() ,
,![]()
![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c.已知cosA= ![]() ,sinB=
,sinB= ![]() C.
C.
(1)求tanC的值;
(2)若a= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某印刷廠為了研究單冊書籍的成本![]() (單位:元)與印刷冊數
(單位:元)與印刷冊數![]() (單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
(單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
印刷冊數 |
|
|
|
|
|
單冊成本 |
|
|
|
|
|
根據以上數據,技術人員分別借助甲、乙兩種不同的回歸模型,得到兩個回歸方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務.
①完成下表(計算結果精確到![]() );
);
印刷冊數 |
|
|
|
|
| |
單冊成本 |
|
|
|
|
| |
模型甲 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
模型乙 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
②分別計算模型甲與模型乙的殘差平方和,并通過比較,判斷哪個模型擬合效果更好.
(2)該書上市之后,受到廣大讀者熱烈歡迎,不久便全部售罄,于是印刷廠決定進行二次印刷,根據市場調查,新需求量為![]() 千冊,若印刷廠以每冊
千冊,若印刷廠以每冊![]() 元的價格將書籍出售給訂貨商,求印刷廠二次印刷
元的價格將書籍出售給訂貨商,求印刷廠二次印刷![]() 千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著互聯網的迅速發展,越來越多的消費者開始選擇網絡購物這種消費方式某營銷部門統計了2019年某月錦州的十大特產的網絡銷售情況得到網民對不同特產的最滿意度![]() 和對應的銷售額
和對應的銷售額![]() (萬元)數據,如下表:
(萬元)數據,如下表:
特產種類 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最滿意度 |
|
|
|
|
|
|
|
|
|
|
銷售額 |
|
|
|
|
|
|
|
|
|
|
![]() 求銷量額
求銷量額![]() 關于最滿意度
關于最滿意度![]() 的相關系數
的相關系數![]() ;
;
![]() 我們約定:銷量額
我們約定:銷量額![]() 關于最滿意度
關于最滿意度![]() 的相關系數
的相關系數![]() 的絕對值在
的絕對值在![]() 以上(含
以上(含![]() )是線性相關性較強;否則,線性相關性較弱.如果沒有達到較強線性相關,則采取“末位淘汰”制(即銷售額最少的特產退出銷售),并求在剔除“末位淘汰”的特產后的銷量額
)是線性相關性較強;否則,線性相關性較弱.如果沒有達到較強線性相關,則采取“末位淘汰”制(即銷售額最少的特產退出銷售),并求在剔除“末位淘汰”的特產后的銷量額![]() 關于最滿意度
關于最滿意度![]() 的線性回歸方程(系數精確到
的線性回歸方程(系數精確到![]() ).
).
參考數據:![]()
![]() ,
,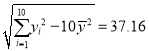 ,
,![]() ,
,![]() .
.
附:對于一組數據![]() .其回歸直線方程
.其回歸直線方程![]() 的斜率和截距的最小二乘法估計公式分別為:
的斜率和截距的最小二乘法估計公式分別為: ,
,![]() .線性相關系數
.線性相關系數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了變廢為寶,節約資源,新上了一個從生活垃圾中提煉生物柴油的項目.經測算該項目月處理成本![]() (元)與月處理量
(元)與月處理量![]() (噸)之間的函數關系可以近似地表示為:
(噸)之間的函數關系可以近似地表示為: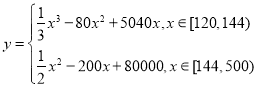 ,且每處理一噸生活垃圾,可得到能利用的生物柴油價值為
,且每處理一噸生活垃圾,可得到能利用的生物柴油價值為![]() 元,若該項目不獲利,政府將給予補貼.
元,若該項目不獲利,政府將給予補貼.
(1)當![]() 時,判斷該項目能否獲利?如果獲利,求出最大利潤;如果不獲利,則政府每月至少需要補貼多少元才能使該項目不虧損?
時,判斷該項目能否獲利?如果獲利,求出最大利潤;如果不獲利,則政府每月至少需要補貼多少元才能使該項目不虧損?
(2)該項目每月處理量為多少噸時,才能使每噸的平均處理成本最低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查我市在校中學生參加體育運動的情況,從中隨機抽取了16名男同學和14 名女同學,調查發現,男、女同學中分別有12人和6人喜愛運動,其余不喜愛.
(1)根據以上數據完成以下![]() 列聯表:
列聯表:
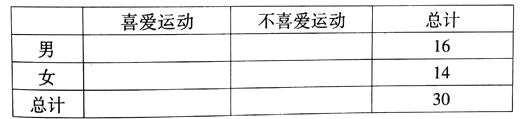
(2)根據列聯表的獨立性檢驗,能否在犯錯誤的概率不超過0.010的前提下認為性別與喜愛運動有關?
(3)將以上統計結果中的頻率視作概率,從我市中學生中隨機抽取3人,若其中喜愛運動的人數為![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某開發區一家汽車生產企業計劃引進一批新能源汽車制造設備,通過市場分析,全年需投入固定成本3000萬元,每生產x(百輛),需另投入成本![]() 萬元,且
萬元,且 ,由市場調研知,每輛車售價6萬元,且全年內生產的車輛當年能全部銷售完.
,由市場調研知,每輛車售價6萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2019年的利潤![]() (萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額
(萬元)關于年產量x(百輛)的函數關系式;(利潤=銷售額![]() 成本)
成本)
(2)2019年產量為多少(百輛)時,企業所獲利潤最大?并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com