【題目】圖是正方體的平面展開圖，在這個正方體中：① 
與 
平行；② 
與 
是異面直線；③ 與 成 
角；④ 
與 
垂直；以上四個命題中，正確的是（ ）
A.①②③
B.②④
C.②③④
D.③④
【答案】D
【解析】解：由已知中正方體的平面展開圖，
得到正方體的直觀圖如下圖所示：
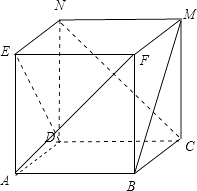
由正方體的幾何特征可得：
①BM與ED平行，不正確；
②CN與BE是異面直線，不正確，是平行線；
③AN∥BM，所以，CN與BM所成的角就是∠ANC=60°角，正確；
④DM與BN垂直，DM與BN垂直，正確；
所以答案是：D．
【考點精析】掌握異面直線及其所成的角和異面直線的判定是解答本題的根本，需要知道異面直線所成角的求法：1、平移法：在異面直線中的一條直線中選擇一特殊點，作另一條的平行線；2、補形法：把空間圖形補成熟悉的或完整的幾何體，如正方體、平行六面體、長方體等，其目的在于容易發現兩條異面直線間的關系；過平面外一點與平面內一點的直線和平面內不經過該點的直線是異面直線.（不在任何一個平面內的兩條直線）．
科目：高中數學 來源： 題型：
【題目】某某車站在春運期間為了改進服務，隨機抽樣調查了100名旅客從開始在購票窗口排隊到購到車票所用的時間t(以下簡稱購票用時，單位：min)．下面是這次抽樣的頻率分布表和頻率分布直方圖，解答下列問題：
分組 | 頻數 | 頻率 | |
一組 | 0≤t<5 | 0 | 0 |
二組 | 5≤t<10 | 10 | |
三組 | 10≤t<15 | 10 | 0.10 |
四組 | 15≤t<20 | ||
五組 | 20≤t<25 | 30 | 0.30 |
合計 | 100 | 1.00 | |
(1)這次抽樣的樣本容量是多少？
(2)在表中填寫缺失的數據并補全頻率分布直方圖．
(3)旅客購票用時的平均數可能落在哪一個小組？
(4)若每增加一個購票窗口可使平均購票用時縮短5 min，要使平均購票用時不超過10 min，那么你估計最少要增加幾個窗口？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某居民區隨機抽取10個家庭，獲得第
個家庭的月收入
（單位：千元）與月儲蓄
（單位：千元）的數據資料，算得
， 
，
， 
(1).求家庭的月儲蓄
對月收入
的線性回歸方程
；
(2).判斷變量
與
之間的正相關還是負相關；
(3).若該居民區某家庭月收入為7千元，預測該家庭的月儲蓄.
附：回歸直線的斜率和截距的最小二乘估計公式分別為
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直三棱柱 
中，底面 
是邊長為2的正三角形， 
是棱 
的中點，且 
.
（1）試在棱 
上確定一點 
，使 
平面 
；
（2）當點 在棱 中點時，求直線 
與平面 
所成角的大小的正弦值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將紅、黑、藍、白5張紙牌（其中白紙牌有2張）隨機分發給甲、乙、丙、丁4個人，每人至少分得1張，則下列兩個事件為互斥事件的是（ ）
A. 事件“甲分得1張白牌”與事件“乙分得1張紅牌”
B. 事件“甲分得1張紅牌”與事件“乙分得1張藍牌”
C. 事件“甲分得1張白牌”與事件“乙分得2張白牌”
D. 事件“甲分得2張白牌”與事件“乙分得1張黑牌”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：對于函數
，若在定義域內存在實數
，滿足
，則稱為“局部奇函數”．
（1）已知二次函數
，試判斷是否為定義域
上的“局部奇函數”?若是，求出所有滿足的的值；若不是，請說明事由．
（2）若
是定義在區間
上的“局部奇函數”，求實數
的取值范圍．
（3）若
為定義域上的“局部奇函數”，求實數的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“奶茶妹妹”對某時間段的奶茶銷售量及其價格進行調查，統計出售價x元和銷售量y杯之間的一組數據如下表所示：
價格x | 5 | 5.5 | 6.5 | 7 |
銷售量y | 12 | 10 | 6 | 4 |
通過分析，發現銷售量y對奶茶的價格x具有線性相關關系．
（Ⅰ）求銷售量y對奶茶的價格x的回歸直線方程；
（Ⅱ）欲使銷售量為13杯，則價格應定為多少？
注：在回歸直線y= 
中， 
， 
= 
﹣ 
． 
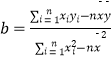=146.5．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
