
【題目】如圖,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC=2.
(1)求證:平面AEF⊥平面PBC;
(2)求三棱錐P﹣AEF的體積.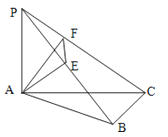
【答案】
解:(1)∵PA⊥平面ABC,BC平面ABC
∴PA⊥BC
又AB⊥BC
∴BC⊥平面PAB,而AE平面PAB
∴BC⊥AE
又AE⊥PB
∴AE⊥平面PBC
而AE平面AEF
∴平面平面AEF⊥平面PBC
(2)由(1)AE⊥平面PBC
又∵AF⊥PC
∴EF⊥PC(三垂線定理逆定理)
∴△PEF∽△PCB
∴![]()
∴S△PEF=![]() S△PBC=
S△PBC=![]()
∴VP﹣AEF=VA﹣PEF=![]() ×
×![]() ×
×![]() =
=![]()
【解析】(1)先根據條件得到PA⊥BC進而得BC⊥平面PAB,把問題轉化為證AE⊥平面PBC即可;
(2)先根據第一問的結論以及三垂線定理逆定理可得△PEF∽△PCB,求出S△PEF , 再利用體積相等即可求出結論.
【考點精析】關于本題考查的平面與平面垂直的判定,需要了解一個平面過另一個平面的垂線,則這兩個平面垂直才能得出正確答案.


科目:高中數學 來源: 題型:
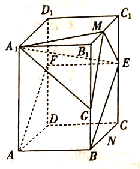
【題目】如圖,四邊形![]() 是正四棱柱
是正四棱柱![]() 的一個截面,此截面與棱
的一個截面,此截面與棱![]() 交于點
交于點![]() ,
, ![]() ,其中
,其中![]() 分別為棱
分別為棱![]() 上一點.
上一點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)![]() 為線段
為線段![]() 上一點,若四面體
上一點,若四面體![]() 與四棱錐
與四棱錐![]() 的體積相等,求
的體積相等,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為 (為參數).在以坐標原點為極點,軸的正半軸為極軸的極坐標系中,曲線
(為參數).在以坐標原點為極點,軸的正半軸為極軸的極坐標系中,曲線![]() :
: ![]() .
.
(Ⅰ)求曲線![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若![]() 與
與![]() 相交于
相交于![]() 兩點,設點
兩點,設點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)的定義域為R,且f(x)不為常值函數,有以下命題:
①函數g(x)=f(x)+f(﹣x)一定是偶函數;
②若對任意x∈R都有f(x)+f(2﹣x)=0,則f(x)是以2為周期的周期函數;
③若f(x)是奇函數,且對于任意x∈R,都有f(x)+f(2+x)=0,則f(x)的圖象的對稱軸方程為x=2n+1(n∈Z);
④對于任意的x1 , x2∈R,且x1≠x2 , 若![]() >0恒成立,則f(x)為R上的增函數,
>0恒成立,則f(x)為R上的增函數,
其中所有正確命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中有這樣一則問題:“今有良馬與弩馬發長安,至齊,齊去長安三千里,良馬初日行一百九十三里,日增一十三里;弩馬初日行九十七里,日減半里,良馬先至齊,復還迎弩馬.”則現有如下說法:
①弩馬第九日走了九十三里路;
②良馬前五日共走了一千零九十五里路;
③良馬和弩馬相遇時,良馬走了二十一日.
則以上說法錯誤的個數是( )個
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四組中,f(x)與g(x)表示同一函數的是( )
A.f(x)=x, ![]()
B.f(x)=x, ![]()
C.f(x)=x2 , ![]()
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,且f(x)在(﹣∞,0]上單調遞減,則不等式f(lgx)>f(﹣2)的解集是( )
A.( ![]() ,100)
,100)
B.(100,+∞)
C.( ![]() ,+∞)
,+∞)
D.(0, ![]() )∪(100,+∞)
)∪(100,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有若干(大于20)件某種自然生長的中藥材,從中隨機抽取20件,其重量都精確到克,規定每件中藥材重量不小于15克為優質品.如圖所示的程序框圖表示統計20個樣本中的優質品數,其中![]() 表示每件藥材的重量,則圖中①,②兩處依次應該填的整數分別是____________.
表示每件藥材的重量,則圖中①,②兩處依次應該填的整數分別是____________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】集合A={(x,y)|y=a},集合B={(x,y)|y=bx+1,b>0,b≠1},若集合A∩B≠,則實數a的取值范圍是( )
A.(﹣∞,1)
B.(﹣∞,1]
C.[1,+∞)
D.(1,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com