Question

【題目】近幾年，電商行業的蓬勃發展帶動了快遞業的迅速增長，快遞公司攬收價格一般是采用“首重+續重”的計價方式.首重是指最低的計費重量，續重是指超過首重部分的計費重量，不滿一公斤按一公斤計費.某快遞網點將快件的攬收價格定為首重（不超過一公斤）8元，續重2元/公斤（例如，若一個快件的重量是0.6公斤，按8元計費；若一個快件的重量是1.4公斤，按元元元計費）.根據歷史數據，得到該網點攬收快件重量的頻率分布直方圖如下圖所示

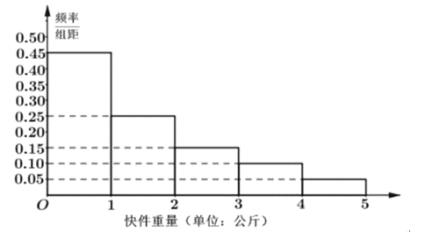
（1）根據樣本估計總體的思想，將頻率視作概率，求該網點攬收快件的平均價格；

（2）為了獲得更大的利潤，該網點對“一天中收發一件快遞的平均成本（單位：元）與當天攬收的快遞件數（單位：百件）之間的關系”進行調查研究，得到相關數據如下表：

每天攬收快遞件數（百件）	2	3	4	5	8
每件快遞的平均成本（元）	5.6	4.8	4.4	4.3	4.1

根據以上數據，技術人員分別根據甲、乙兩種不同的回歸模型，得到兩個回歸方程：

方程甲：，方程乙：.

①為了評價兩種模型的擬合效果，根據上表數據和相應回歸方程，將以下表格填寫完整（結果保留一位小數），分別計算模型甲與模型乙的殘差平方和，，并依此判斷哪個模型的擬合效果更好（備注：稱為相應于點的殘差，殘差平方和；

每天攬收快遞件數/百件		2	3	4	5	8
每天快遞的平均成本/元		5.6	4.8	4.4	4.3	4.1
模型甲	預報值	5.2	5.0	4.8
	殘差		0.2	0.4
模型乙	預報值	5.5	4.8	4.5
	預報值		0	0.1

②預計該網點今年6月25日（端午節）一天可以攬收1000件快遞，試根據①中確定的擬合效果較好的回歸模型估計該網點當天的總利潤（總利潤=（平均價格-平均成本）×總件數）.

Answer 1

【答案】（1）元（2）①填表見解析；；；模型乙的擬合效果較好②元

【解析】

（1）根據頻率分布直方圖得出快件價格的頻率分布表，再計算平均價格；

（2）①分別把代入兩模型方程，計算預報值和殘差平方和；

②把代入回歸方程，得出平均成本，再計算利潤．

解：（1）根據攬收快件重量的頻率分布直方圖，得到其價格的頻率分布表如下：

價格	8	10	12	14	16
頻率	0.45	0.25	0.15	0.1	0.05

所以平均價格為

元.

（2）①表中數據填寫如下：

每天攬收快遞件數/百件		2	3	4	5	8
每件快遞的平均成本/元		5.6	4.8	4.4	4.3	4.1
模型甲	預報值	5.2	5.0	4.8	4.6	4.0
	殘差		0.2	0.4	0.3
模型乙	預報值	5.5	4.8	4.5	4.3	4.0
	殘差		0	0.1	0

計算可得：；

.

因為，所以模型乙的擬合效果較好.

②模型乙的回歸方程為，

當一天攬收件數為1000時，則收發一件快遞的平均成本為，

可以估計該網點當天的總利潤為元.