
【題目】為了更好地貫徹黨的“五育并舉”的教育方針,某市要對全市中小學生“體能達標”情況進行了解,決定通過隨機抽樣選擇幾個樣本校對學生進行體能達標測試,并規定測試成績低于60分為不合格,否則為合格,若樣本校學生不合格人數不超過其總人數的5%,則該樣本校體能達標為合格.已知某樣本校共有1000名學生,現從中隨機抽取40名學生參加體能達標測試,首先將這40名學生隨機分為甲、乙兩組,其中甲乙兩組學生人數的比為3:2,測試后,兩組各自的成績統計如下:甲組的平均成績為70,方差為16,乙組的平均成績為80,方差為36.
(1)估計該樣本校學生體能測試的平均成績;
(2)求該樣本校40名學生測試成績的標準差s;
(3)假設該樣本校體能達標測試成績服從正態分布![]() ,用樣本平均數
,用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差s作為
,用樣本標準差s作為![]() 的估計值
的估計值![]() ,利用估計值估計該樣本校學生體能達標測試是否合格?
,利用估計值估計該樣本校學生體能達標測試是否合格?
(注:1.本題所有數據的最后結果都精確到整數;2若隨機變量z服從正態分布,則![]() ,
,![]() ,
,![]() )
)
【答案】(1)74;(2)![]() .(3)可估計該樣本校學生“體能達標”測試合格.
.(3)可估計該樣本校學生“體能達標”測試合格.
【解析】
(1)由甲乙兩組學生人數可求得總均分;
(2)設第一組學生的測試成績分別為![]() ,第二組學生的測試成績分別為
,第二組學生的測試成績分別為![]() ,由已知方差求得
,由已知方差求得![]() 和
和![]() ,結合(1)可得總方差;
,結合(1)可得總方差;
(3)由已知數據知![]() ,然后求出不合格的概率得不合格人數,從而得結論.
,然后求出不合格的概率得不合格人數,從而得結論.
解:(1)由題知,甲、乙兩組學生數分別為24和16,
則這40名學生測試成績的平均分![]()
故可估計該樣本校學生體能測試的平均成績為74,.
(2)由![]() 變形得
變形得![]()
設第一組學生的測試成績分別為![]() ,
,
第二組學生的測試成績分別為![]() ,
,
則第一組的方差為
![]() ,
,
解得![]() .
.
第二組的方差為
![]()
解得![]() .
.
這40名學生的方差為
![]()
![]() ,
,
所以![]() .
.
綜上,標準差![]() .
.
(3)由![]() ,
,![]() ,得
,得![]() 的估計值為
的估計值為![]() ,
,![]() 的估計值
的估計值![]()
由![]() ,
,
得![]() ,
,
即![]()
所以![]() .
.
從而,在全校1000名學生中,“不合格”的有![]() (人)
(人)
而![]() ,
,
故可估計該樣本校學生“體能達標”測試合格.


科目:高中數學 來源: 題型:
【題目】近幾年,電商行業的蓬勃發展帶動了快遞業的迅速增長,快遞公司攬收價格一般是采用“首重+續重”的計價方式.首重是指最低的計費重量,續重是指超過首重部分的計費重量,不滿一公斤按一公斤計費.某快遞網點將快件的攬收價格定為首重(不超過一公斤)8元,續重2元/公斤(例如,若一個快件的重量是0.6公斤,按8元計費;若一個快件的重量是1.4公斤,按![]() 元
元![]() 元
元![]() 元計費).根據歷史數據,得到該網點攬收快件重量的頻率分布直方圖如下圖所示
元計費).根據歷史數據,得到該網點攬收快件重量的頻率分布直方圖如下圖所示
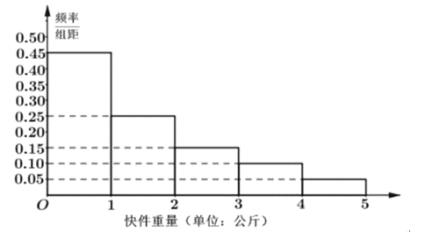
(1)根據樣本估計總體的思想,將頻率視作概率,求該網點攬收快件的平均價格;
(2)為了獲得更大的利潤,該網點對“一天中收發一件快遞的平均成本![]() (單位:元)與當天攬收的快遞件數
(單位:元)與當天攬收的快遞件數![]() (單位:百件)
(單位:百件)![]() 之間的關系”進行調查研究,得到相關數據如下表:
之間的關系”進行調查研究,得到相關數據如下表:
每天攬收快遞件數 | 2 | 3 | 4 | 5 | 8 |
每件快遞的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
根據以上數據,技術人員分別根據甲、乙兩種不同的回歸模型,得到兩個回歸方程:
方程甲:![]() ,方程乙:
,方程乙:![]() .
.
①為了評價兩種模型的擬合效果,根據上表數據和相應回歸方程,將以下表格填寫完整(結果保留一位小數),分別計算模型甲與模型乙的殘差平方和![]() ,
,![]() ,并依此判斷哪個模型的擬合效果更好(備注:
,并依此判斷哪個模型的擬合效果更好(備注:![]() 稱為相應于點
稱為相應于點![]() 的殘差,殘差平方和
的殘差,殘差平方和![]() ;
;
每天攬收快遞件數 | 2 | 3 | 4 | 5 | 8 | |
每天快遞的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
模型甲 | 預報值 | 5.2 | 5.0 | 4.8 | ||
殘差 |
| 0.2 | 0.4 | |||
模型乙 | 預報值 | 5.5 | 4.8 | 4.5 | ||
預報值 |
| 0 | 0.1 | |||
②預計該網點今年6月25日(端午節)一天可以攬收1000件快遞,試根據①中確定的擬合效果較好的回歸模型估計該網點當天的總利潤(總利潤=(平均價格-平均成本)×總件數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動直線
中,動直線![]() 交拋物線
交拋物線![]() 于A,B兩點.
于A,B兩點.
(1)若![]() ,證明直線
,證明直線![]() 過定點,并求出該定點;
過定點,并求出該定點;
(2)點M為![]() 的中點,過點M作與y軸垂直的直線交拋物線
的中點,過點M作與y軸垂直的直線交拋物線![]() 于C點;點N為
于C點;點N為![]() 的中點,過點N作與y軸垂直的直線交拋物線
的中點,過點N作與y軸垂直的直線交拋物線![]() 于點P.設△
于點P.設△![]() 的面積
的面積![]() ,△
,△![]() 的面積為
的面積為![]() .
.
(i)若![]() 過定點
過定點![]() ,求使
,求使![]() 取最小值時,直線
取最小值時,直線![]() 的方程;
的方程;
(ii)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,PA⊥平面ABCD,PA=AB,E為線段PB的中點,F為線段BC上的動點.

(1)求證:AE⊥平面PBC;
(2)試確定點F的位置,使平面AEF與平面PCD所成的銳二面角為30°.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]() (
(![]() 為參數,
為參數,![]() ).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的圾坐標方
).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的圾坐標方![]() ,且直線l與曲線C相交于A,B兩點.
,且直線l與曲線C相交于A,B兩點.
(1)求曲線C的普通方程和l的直角坐標方程;
(2)若![]() ,點
,點![]() 滿足
滿足![]() ,求此時r的值.
,求此時r的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解高新產業園引進的甲公司前期的經營狀況,市場研究人員對該公司2019年下半年連續六個月的利潤進行了統計,統計數據列表如下:
月份 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
月利潤(萬元) | 110 | 130 | 160 | 150 | 200 | 210 |
(1)請用相關系數說明月利潤y(單位:萬元)與月份代碼x之間的關系的強弱(結果保留兩位小數),求y關于x的線性回歸方程,并預測該公司2020年1月份的利潤;
(2)甲公司新研制了一款產品,需要采購一批新型材料,己知生產新型材料的乙企業對A、B兩種型號各100件新型材料進行模擬測試,統計兩種新型材料使用壽命頻數如下表所示:
使用壽命 材料類型 | 1個月 | 2個月 | 3個月 | 4個月 | 總計 |
A | 15 | 40 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
現有采購成本分別為10萬元/件和12萬元/件的A、B兩種型號的新型材料可供選擇,按規定每種新型材料最多可使用4個月,不同類型的新型材料損壞的時間各不相同,經甲公司測算,平均每件新型材料每月可以帶來5萬元收入,不考慮除采購成本之外的其他成本,假設每件新型材料的使用壽命都是整數月,且以頻率估計每件新型材料使用壽命的概率,如果你是甲公司的負責人,以每件新型材料產生利潤的期望值為決策依據,你會選擇采購哪款新型材料?
參考公式:相關系數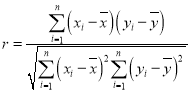 ;
;
回歸直線方程為![]() ,其中
,其中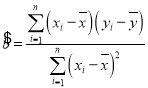 ,
,![]() .
.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的各項均為不等的正整數,其前
的各項均為不等的正整數,其前![]() 項和為
項和為![]() ,我們稱滿足條件“對任意的
,我們稱滿足條件“對任意的![]() ,均有
,均有![]() ”的數列
”的數列![]() 為“好”數列.
為“好”數列.
(1)試分別判斷數列![]() ,
,![]() 是否為“好”數列,其中
是否為“好”數列,其中![]() ,
,![]() ,
,![]() ,并給出證明;
,并給出證明;
(2)已知數列![]() 為“好”數列.
為“好”數列.
① 若![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
② 若![]() ,且對任意給定正整數
,且對任意給定正整數![]() (
(![]() ),有
),有![]() 成等比數列,求證:
成等比數列,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,圓
,圓![]() 經過橢圓
經過橢圓![]() 的左,右焦點
的左,右焦點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 的垂直平分線與
的垂直平分線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得
,使得![]() 的面積與
的面積與![]() (
(![]() 為原點)的面積相等?若存在,求出
為原點)的面積相等?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的定義域為
的定義域為![]() ,其圖象如圖所示.函數
,其圖象如圖所示.函數![]() 是定義域為
是定義域為![]() 的奇函數,滿足
的奇函數,滿足![]() ,且當
,且當![]() 時,
時,![]() .給出下列三個結論:
.給出下列三個結論:
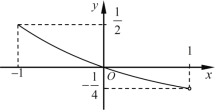
①![]() ;
;
②函數![]() 在
在![]() 內有且僅有
內有且僅有![]() 個零點;
個零點;
③不等式![]() 的解集為
的解集為![]() .
.
其中,正確結論的序號是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com