
(本小題滿分12分)
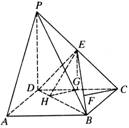
 如圖,四棱錐P-ABCD的底面為矩形,側(cè)棱PD垂直于底面,PD=DC=2BC,E為棱PC上的點,且平面BDE⊥平面PBC.
如圖,四棱錐P-ABCD的底面為矩形,側(cè)棱PD垂直于底面,PD=DC=2BC,E為棱PC上的點,且平面BDE⊥平面PBC.
(1)求證:E為PC的中點;
(2)求二面角A-BD-E的大小.
解法一:(1)證明:如圖,作CF⊥BE,垂足為F,
由平面BDE⊥平面PBC,
則CF⊥平面BDE,知CF⊥DE.
因為PD⊥平面ABCD,BC⊥CD,
 CD為DE在平面ABCD內(nèi)的射影,
CD為DE在平面ABCD內(nèi)的射影,
所以BC⊥DE,所以DE⊥平面PBC.
于是DE⊥PC,又PD=PC,所以E為PC的中點.………………6分
(2)作EG⊥DC,垂足為G,則EG∥PD,從而EG⊥平面ABCD.
作GH⊥BD,垂足為H,連接EH,則BD⊥EH,
故∠EHG為二面角A-BD-E的平面角的補角.…………………9分
不妨設(shè)BC=1,則PD=DC=2,
在Rt△EGH中,EG=![]() PD=1,
PD=1,
GH=![]() =
=![]() ,
,
∴tan∠EHC=![]() =
=![]() .
.
因此二面角A-BD-E的大小為![]() -arctan
-arctan![]() .……………………12分
.……………………12分
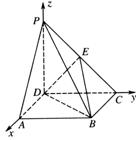 解法二:不妨設(shè)BC=1,則PD=DC=2.
解法二:不妨設(shè)BC=1,則PD=DC=2.
建立如圖所示的空間直角坐標(biāo)系D-xyz,
則D(0,0,0),B(1,2,0),C(0,2,0),P(0,0,2).
(1)證明:設(shè)![]() =
=![]() ,則E(0,
,則E(0,![]() ,
,![]() ).
).
設(shè)a= (x1,y1,z1)為面PBC的法向量,
則a⊥![]() ,a⊥
,a⊥![]() ,
,
又![]() =(1,0,0),
=(1,0,0),![]() =(0,-2,2),
=(0,-2,2),
∴a![]() =x1=0,a
=x1=0,a![]() =-2y1+2z1=0,
=-2y1+2z1=0,
取a=(0,1,1).
設(shè)b=(x2,y2,z2)為面BDE的法向量,
則b⊥![]() ,b⊥
,b⊥![]() ,
,
又![]() =(1,2,0),
=(1,2,0),![]() =(0,
=(0,![]() ,
,![]() ),
),
∴b![]() =x2+2y2=0,b
=x2+2y2=0,b![]() =
=![]() +
+![]() =0,
=0,
取b=(![]() ,
,![]() ,1).
,1).
∵平面BDE⊥平面PBC,
∴a·b=![]() +1=0,
+1=0,![]() =1.
=1.
所以E為PC的中點.…………………………………………6分
(2)由(Ⅰ)知,b=(2,-1,1)為面BDE的法向量,
又c=(0,0,1)為面ADB的法向量,
∵cos<b,c>=![]() =
=![]() ,
,
所以二面角A-BD-E的大小為![]() -arccos
-arccos![]() .………………12分
.………………12分


 小學(xué)學(xué)習(xí)好幫手系列答案
小學(xué)學(xué)習(xí)好幫手系列答案 小學(xué)同步三練核心密卷系列答案
小學(xué)同步三練核心密卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(2009湖南卷文)(本小題滿分12分)
為拉動經(jīng)濟增長,某市決定新建一批重點工程,分別為基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程三類,這三類工程所含項目的個數(shù)分別占總數(shù)的![]() 、
、![]() 、
、![]() .現(xiàn)有3名工人獨立地從中任選一個項目參與建設(shè).求:
.現(xiàn)有3名工人獨立地從中任選一個項目參與建設(shè).求:
(I)他們選擇的項目所屬類別互不相同的概率; w.w.w.k.s.5.u.c.o.m ![]()
![]()
(II)至少有1人選擇的項目屬于民生工程的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分12分)
某民營企業(yè)生產(chǎn)A,B兩種產(chǎn)品,根據(jù)市場調(diào)查和預(yù)測,A產(chǎn)品的利潤與投資成正比,其關(guān)系如圖1,B產(chǎn)品的利潤與投資的算術(shù)平方根成正比,其關(guān)系如圖2,
(注:利潤與投資單位是萬元)
(1)分別將A,B兩種產(chǎn)品的利潤表示為投資的函數(shù),并寫出它們的函數(shù)關(guān)系式.(2)該企業(yè)已籌集到10萬元資金,并全部投入到A,B兩種產(chǎn)品的生產(chǎn),問:怎樣分配這10萬元投資,才能使企業(yè)獲得最大利潤,其最大利潤為多少萬元.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com