
已知 =(
=(![]() ,
,![]() ),
),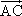 =(-2,y),若
=(-2,y),若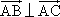 ,則y的值為
,則y的值為
![]()
-2
![]()
2
科目:高中數學 來源:甘肅省張掖中學2012屆高三第二次月考數學理科試題 題型:013
已知![]() =b,則常數a、b的值分別為
=b,則常數a、b的值分別為
a
=2,b=-4a
=-2,b=4a
=a
=-查看答案和解析>>
科目:高中數學 來源:2012-2013學年陜西省高三上學期第一次模擬考試理科數學試卷(解析版) 題型:填空題
已知 =2·
=2· ,
, =3·
=3· ,
, =4·
=4· ,….若
,….若 =8·
=8· (
(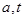 均為正實數),類比以上等式,可推測
均為正實數),類比以上等式,可推測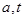 的值,則
的值,則 = .
= .
查看答案和解析>>
科目:高中數學 來源:2012-2013學年陜西省高三上學期第一次模擬考試文科數學試卷(解析版) 題型:填空題
已知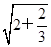 =2·
=2·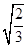 ,
, =3·
=3·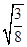 ,
, 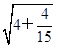 =4·
=4·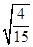 ,….若
,….若 =8·
=8·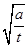 (
(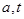 均為正實數),類比以上等式,可推測
均為正實數),類比以上等式,可推測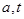 的值,則
的值,則 = .
= .
查看答案和解析>>
科目:高中數學 來源:2012年人教A版高中數學必修四2.2平面向量的線性運算練習卷(一)(解析版) 題型:選擇題
已知平行四邊形ABCD,設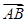 +
+ +
+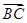 +
+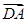 =a,而b是一非零向量,則下列結論正確的有( )
=a,而b是一非零向量,則下列結論正確的有( )
①a∥b ②a+b=a
③a+b=b ④|a+b|<|a|+|b|
A.①③ B.②③
C.②④ D.①②
查看答案和解析>>
科目:高中數學 來源:2014屆廣東省高一期中考試文科數學試卷A卷(解析版) 題型:解答題
已知函數f(x)(x∈R)滿足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的實數x只有一個.
,a≠0,f(1)=1,且使f(x)=2x成立的實數x只有一個.
(1)求函數f(x)的表達式;
(2)若數列{an}滿足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,證明數列{bn}是等比數列,并求出{bn}的通項公式;
-1,n∈N*,證明數列{bn}是等比數列,并求出{bn}的通項公式;
(3)在(2)的條件下,證明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}為等比數列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)證明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com