
【題目】為慶祝黨的98歲生日,某高校組織了“歌頌祖國,緊跟黨走”為主題的黨史知識競賽。從參加競賽的學生中,隨機抽取40名學生,將其成績分為六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如圖所示的頻率分布直方圖.
,到如圖所示的頻率分布直方圖.

(1)求圖中![]() 的值及樣本的中位數與眾數;
的值及樣本的中位數與眾數;
(2)若從競賽成績在![]() 與
與![]() 兩個分數段的學生中隨機選取兩名學生,設這兩名學生的競賽成績之差的絕對值不大于
兩個分數段的學生中隨機選取兩名學生,設這兩名學生的競賽成績之差的絕對值不大于![]() 分為事件
分為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
(3)為了激勵同學們的學習熱情,現評出一二三等獎,得分在![]() 內的為一等獎,得分在
內的為一等獎,得分在![]() 內的為二等獎, 得分在
內的為二等獎, 得分在![]() 內的為三等獎.若將頻率視為概率,現從考生中隨機抽取三名,設
內的為三等獎.若將頻率視為概率,現從考生中隨機抽取三名,設![]() 為獲得三等獎的人數,求
為獲得三等獎的人數,求![]() 的分布列與數學期望.
的分布列與數學期望.
【答案】(1)0.06;87.5;87.5;(2)![]() ;(3)詳見解析
;(3)詳見解析
【解析】
(1)根據小矩形的面積之和等于1,列出方程,求得![]() 的值,根據中位數定義估計中位數的范圍,在列出方程求解中位數,再根據眾數的定義,即可求解.
的值,根據中位數定義估計中位數的范圍,在列出方程求解中位數,再根據眾數的定義,即可求解.
(2)計算兩組的人數,再計算抽取的兩人在同一組的概率,即可求解;
(3)根據題意,得到隨機變量服從二項分布,再利用二項分布的期望公式,即可求解.
(1)由頻率分布直方圖可知![]() ,解得
,解得![]() ,
,
可知樣本的中位數在第4組中,不妨設為![]() ,
,
則![]() ,解得
,解得![]() ,
,
即樣本的中位數為![]() ,
,
由頻率分布直方圖可知,樣本的眾數為![]() .
.
(2)由頻率分布直方圖可知,在![]() 與
與![]() 兩個分數段的學生人數分別為
兩個分數段的學生人數分別為![]() 和
和![]() ,設中兩名學生的競賽成績之差的絕對值不大于5分為事件M,
,設中兩名學生的競賽成績之差的絕對值不大于5分為事件M,
則事件M發生的概率為![]() ,即事件M發生的概率為
,即事件M發生的概率為![]() .
.
(3)從考生中隨機抽取三名,則隨機變量![]() 為獲得三等獎的人數,則
為獲得三等獎的人數,則![]() ,
,
由頻率分布直方圖知,從考升中任抽取1人,此生獲得三等獎的概率為![]() ,
,
所以隨機變量服從二項分布![]() ,
,
則![]() ,
,
![]() ,
,
所以隨機變量的分布列為
| 0 | 1 | 2 | 3 |
| 0.343 | 0.441 | 0.189 | 0.027 |
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖:

(2)估計該家庭使用節水龍頭后,日用水量小于0.35 m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費10元;重量超過
的包裹收費10元;重量超過![]() 的包裹,除收費10元之外,超過
的包裹,除收費10元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
計算)需要再收費5元.該公司近60天每天攬件數量的頻率分布直方圖如下圖所示(同一組數據用該區間的中點值作代表).
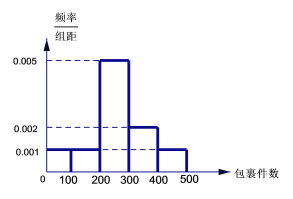
(1)求這60天每天包裹數量的平均值和中位數;
(2)該公司從收取的每件快遞的費用中抽取5元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.已知公司前臺有工作人員3人,每人每天工資100元,以樣本估計總體,試估計該公司每天的利潤有多少元?
(3)小明打算將![]() 四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過
四件禮物隨機分成兩個包裹寄出,且每個包裹重量都不超過![]() ,求他支付的快遞費為45元的概率.
,求他支付的快遞費為45元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點F(1,0),定直線![]() ,動點M到點F的距離與到直線l的距離相等.
,動點M到點F的距離與到直線l的距離相等.
(1)求動點M的軌跡方程;
(2)設點![]() ,過點F作一條斜率大于0的直線交軌跡M于A,B兩點,分別連接PA,PB,若直線PA與直線PB不關于x軸對稱,求實數t的取值范圍.
,過點F作一條斜率大于0的直線交軌跡M于A,B兩點,分別連接PA,PB,若直線PA與直線PB不關于x軸對稱,求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com