
若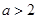 ,則函數
,則函數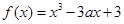 在區間
在區間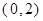 上零點的個數為
上零點的個數為
| A.0個 |
| B.1個 |
| C.2個 |
| D.3個 |
B
解析考點:函數的零點.
分析:根據a>2,分析導函數的符號,確定函數的單調性,驗證f(0),f(2)的符號,結合圖象可知函數f(x)=x3-3ax+3 在(0,2)上的零點個數.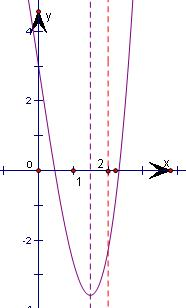
解:∵函數f(x)=x3-3ax+3
∴f′(x)=3x2-3a=3(x2-a)=3(x+ )(x-
)(x- ),
),
∵a>2,
令f′(x)>0得x> ,得函數f(x)在(
,得函數f(x)在( ,+∞)上是增函數,
,+∞)上是增函數,
令f′(x)<0可得0<x< ,得函數f(x)在(0,
,得函數f(x)在(0, )上是減函數,
)上是減函數,
而f(0)=3>0,f( )=(
)=( )3-3a
)3-3a +3=3-2a
+3=3-2a <0,
<0,
∴函數f(x)=x3-3ax+3在(0, )上零點有一個.
)上零點有一個.
又f(2)=23-3a×2+3=11-6a<0,
∴函數f(x)=x3-3ax+3在( ,2)上沒有零點.
,2)上沒有零點.
則函數f(x)=x3-3ax+3在區間(0,2)上零點的個數為1,
故選B.


科目:高中數學 來源: 題型:
| x2 |
| 5 |
| y2 |
| m |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
如右圖(1)所示,定義在區間![]() 上的函數
上的函數![]() ,如果滿
,如果滿
足:對![]() ,
,![]() 常數A,都有
常數A,都有![]() 成立,則稱函數
成立,則稱函數
![]() 在區間
在區間![]() 上有下界,其中
上有下界,其中![]() 稱為函數的下界. (提示:圖(1)、(2)中的常數
稱為函數的下界. (提示:圖(1)、(2)中的常數![]() 、
、![]() 可以是正數,也可以是負數或零)
可以是正數,也可以是負數或零)
 (Ⅰ)試判斷函數
(Ⅰ)試判斷函數![]() 在
在![]() 上是否有下界?并說明理由;
上是否有下界?并說明理由;
(Ⅱ)又如具有右圖(2)特征的函數稱為在區間![]() 上有上界.
上有上界.
請你類比函數有下界的定義,給出函數![]() 在區間
在區間![]() 上
上
有上界的定義,并判斷(Ⅰ)中的函數在![]() 上是否
上是否
有上界?并說明理由;
(Ⅲ)若函數![]() 在區間
在區間![]() 上既有上界又有下界,則稱函數
上既有上界又有下界,則稱函數
![]() 在區間
在區間![]() 上有界,函數
上有界,函數![]() 叫做有界函數.試探究函數
叫做有界函數.試探究函數![]() (
(![]()
![]()
![]() 是常數)是否是
是常數)是否是![]() (
(![]()
![]() 、
、![]() 是常數)上的有界函數?
是常數)上的有界函數?
查看答案和解析>>
科目:高中數學 來源:2010年普通高等學校招生全國統一考試預測卷(廣東卷)理科試題 題型:解答題
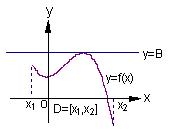
(本小題滿分14分)對于定義在區間D上的函數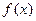 ,若存在閉區間
,若存在閉區間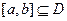 和常數
和常數 ,使得對任意
,使得對任意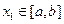 ,都有
,都有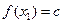 ,且對任意
,且對任意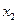 ∈D,當
∈D,當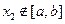 時,
時,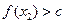 恒成立,則稱函數
恒成立,則稱函數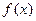 為區間D上的“平底型”函數.
為區間D上的“平底型”函數.
(Ⅰ)判斷函數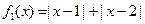 和
和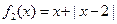 是否為R上的“平底
是否為R上的“平底 型”函數? 并說明理由;
型”函數? 并說明理由;
(Ⅱ)設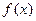 是(Ⅰ)中的“平底型”函數,k為非零常數,若不等式
是(Ⅰ)中的“平底型”函數,k為非零常數,若不等式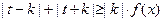 對一切
對一切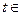 R恒成立,求實數
R恒成立,求實數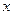 的取值范圍;
的取值范圍;
(Ⅲ)若函數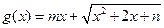 是區間
是區間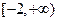 上的“平底型”函數,求
上的“平底型”函數,求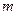 和
和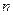 的值.
的值.
.
查看答案和解析>>
科目:高中數學 來源:廣東省09-10學年高二下學期期末考試理科數學試題 題型:解答題
(本小題滿分14分)對于定義在區間D上的函數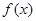 ,若存在閉區間
,若存在閉區間 和常數
和常數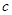 ,使得對任意
,使得對任意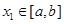 ,都有
,都有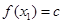 ,且對任意
,且對任意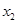 ∈D,當
∈D,當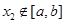 時,
時,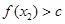 恒成立,則稱函數
恒成立,則稱函數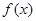 為區間D上的“平底型”函數.
為區間D上的“平底型”函數.
(Ⅰ)判斷函數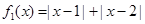 和
和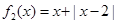 是否為R上的“平底型”函數?并說明理由;
是否為R上的“平底型”函數?并說明理由;
(Ⅱ)設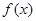 是(Ⅰ)中的“平底型”函數,k為非零常數,若不等式
是(Ⅰ)中的“平底型”函數,k為非零常數,若不等式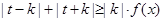 對一切
對一切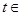 R恒成立,求實數
R恒成立,求實數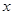 的取值范圍;
的取值范圍;
(Ⅲ)若函數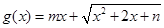 是區間
是區間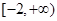 上的“平底型”函數,求
上的“平底型”函數,求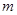 和
和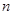 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省廈門市高三上學期末理科數學卷 題型:選擇題
設函數 的定義域為D,若存在非零實數h使得對于任意
的定義域為D,若存在非零實數h使得對于任意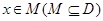 ,有
,有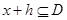 ,且
,且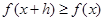 ,則稱
,則稱 為M上的“h階高調函數”。給出如下結論:
為M上的“h階高調函數”。給出如下結論:
①若函數 在R上單調遞增,則存在非零實數h使
在R上單調遞增,則存在非零實數h使 為R上的“h階高調函數”;
為R上的“h階高調函數”;
②若函數 為R上的“h階高調函數”,則
為R上的“h階高調函數”,則 在R上單調遞增;
在R上單調遞增;
③若函數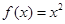 為區間
為區間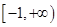 上的“h階高誣蔑財函數”,則
上的“h階高誣蔑財函數”,則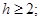
④若函數 在R上的奇函數,且
在R上的奇函數,且 時,
時,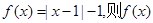 只能是R上的“4階高調函數”。
只能是R上的“4階高調函數”。
其中正確結論的序號為 ( )
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com