
【題目】如圖,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點(diǎn),將四邊形
的中點(diǎn),將四邊形![]() 沿直線
沿直線![]() 進(jìn)行翻折,給出下列四個結(jié)論:①
進(jìn)行翻折,給出下列四個結(jié)論:①![]() ;②
;②![]() ③平面
③平面![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() ,則上述結(jié)論可能正確的是( ).
,則上述結(jié)論可能正確的是( ).
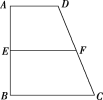
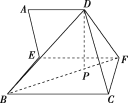
A.①③B.②③C.②④D.③④
【答案】B
【解析】
根據(jù)題意,結(jié)合![]() 與
與![]() 相交但不垂直,可判斷①錯;設(shè)點(diǎn)
相交但不垂直,可判斷①錯;設(shè)點(diǎn)![]() 在平面
在平面![]() 上的射影為點(diǎn)
上的射影為點(diǎn)![]() ,當(dāng)
,當(dāng)![]() 時就有
時就有![]() ,即可滿足條件,判斷②正確;當(dāng)點(diǎn)
,即可滿足條件,判斷②正確;當(dāng)點(diǎn)![]() 在平面
在平面![]() 上的射影
上的射影![]() 落在
落在![]() 上時,根據(jù)面面垂直的判定定理,即可得③正確;根據(jù)點(diǎn)
上時,根據(jù)面面垂直的判定定理,即可得③正確;根據(jù)點(diǎn)![]() 在平面
在平面![]() 上的射影不可能在
上的射影不可能在![]() 上,可判斷④錯.
上,可判斷④錯.
對于①,因為![]() ,
,![]() 與
與![]() 相交但不垂直,所以
相交但不垂直,所以![]() 與
與![]() 不垂直,則①不成立;對于②,設(shè)點(diǎn)
不垂直,則①不成立;對于②,設(shè)點(diǎn)![]() 在平面
在平面![]() 上的射影為點(diǎn)
上的射影為點(diǎn)![]() ,當(dāng)
,當(dāng)![]() 時就有
時就有![]() ,而
,而![]() 可使條件滿足,所以②正確;
可使條件滿足,所以②正確;
對于③,當(dāng)點(diǎn)![]() 在平面
在平面![]() 上的射影
上的射影![]() 落在
落在![]() 上時,
上時,![]() 平面
平面![]() ,從而平面
,從而平面![]() 平面
平面![]() ,所以③正確;
,所以③正確;
對于④,因為點(diǎn)![]() 在平面
在平面![]() 上的射影不可能在
上的射影不可能在![]() 上,所以④不成立.
上,所以④不成立.
故選B



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的圖像在
的圖像在![]() 出的切線方程;
出的切線方程;
(2)判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)P是拋物線C:![]() 上任意一點(diǎn),過點(diǎn)P作直線PH⊥x軸,點(diǎn)H為垂足.點(diǎn)M是直線PH上一點(diǎn),且在拋物線的內(nèi)部,直線l過點(diǎn)M交拋物線C于A、B兩點(diǎn),且點(diǎn)M是線段AB的中點(diǎn).
上任意一點(diǎn),過點(diǎn)P作直線PH⊥x軸,點(diǎn)H為垂足.點(diǎn)M是直線PH上一點(diǎn),且在拋物線的內(nèi)部,直線l過點(diǎn)M交拋物線C于A、B兩點(diǎn),且點(diǎn)M是線段AB的中點(diǎn).
(1)證明:直線l平行于拋物線C在點(diǎn)P處切線;
(2)若|PM|=![]() , 當(dāng)點(diǎn)P在拋物線C上運(yùn)動時,△PAB的面積如何變化?
, 當(dāng)點(diǎn)P在拋物線C上運(yùn)動時,△PAB的面積如何變化?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從拋物線![]() 上任意一點(diǎn)
上任意一點(diǎn)![]() 向
向![]() 軸作垂線段垂足為
軸作垂線段垂足為![]() ,點(diǎn)
,點(diǎn)![]() 是線段
是線段![]() 上的一點(diǎn),且滿足
上的一點(diǎn),且滿足![]() .
.
(1)求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 為軌跡
為軌跡![]() 上異于
上異于![]() 的任意一點(diǎn),直線
的任意一點(diǎn),直線![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點(diǎn).問:
兩點(diǎn).問:![]() 軸正半軸上是否存在定點(diǎn)使得以
軸正半軸上是否存在定點(diǎn)使得以![]() 為直徑的圓過該定點(diǎn)?若存在,求出符合條件的定點(diǎn)坐標(biāo);若不存在,請說明理由.
為直徑的圓過該定點(diǎn)?若存在,求出符合條件的定點(diǎn)坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,正方形![]() 的邊長為
的邊長為![]() ,已知
,已知![]() ,將
,將![]() 沿
沿![]() 邊折起,折起后
邊折起,折起后![]() 點(diǎn)在平面
點(diǎn)在平面![]() 上的射影為
上的射影為![]() 點(diǎn),則翻折后的幾何體中有如下描述:①
點(diǎn),則翻折后的幾何體中有如下描述:①![]() 與
與![]() 所成角的正切值為
所成角的正切值為![]() ;②
;②![]() ;③
;③![]() ;④平面
;④平面![]() 平面
平面![]() ,其中正確的命題序號為___________.
,其中正確的命題序號為___________.
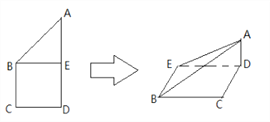
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在三棱臺![]() 中,點(diǎn)
中,點(diǎn)![]() 在
在![]() 上,且
上,且![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 內(nèi)(含邊界)的一個動點(diǎn),且有平面
內(nèi)(含邊界)的一個動點(diǎn),且有平面![]() 平面
平面![]() ,則動點(diǎn)
,則動點(diǎn)![]() 的軌跡是( )
的軌跡是( )

A. 平面B. 直線C. 線段,但只含1個端點(diǎn)D. 圓
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知三棱柱![]() 的側(cè)棱垂直于底面,
的側(cè)棱垂直于底面,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別為
分別為![]() 和
和![]() 的中點(diǎn).
的中點(diǎn).

(1)若![]() ,求三棱柱
,求三棱柱![]() 的體積;
的體積;
(2)證明:![]() 平面
平面![]() ;
;
(3)請問當(dāng)![]() 為何值時,
為何值時,![]() 平面
平面![]() ,試證明你的結(jié)論.
,試證明你的結(jié)論.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com