Question

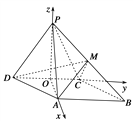
【題目】如圖，在四棱錐P－ABCD中，底面ABCD是菱形，∠ADC＝60°，側(cè)面PDC是正三角形，平面PDC⊥平面ABCD，CD＝2，M為PB的中點.

(1)求證：PA⊥平面CDM．

(2)求二面角D－MC－B的余弦值．

Answer 1

【答案】(1) 見解析；(2)－．

【解析】試題分析：

（1）取DC中點O，連接PO，根據(jù)題意可證得OA，OC，OP兩兩垂直，建立空間直角坐標系，運用坐標法可證得，從而PA⊥DM，PA⊥DC，根據(jù)線面垂直的判定定理可得結(jié)論．（2）結(jié)合（1）可求得平面BMC的一個法向量，又平面CDM的法向量為，求出兩向量夾角的余弦值，結(jié)合圖形可得二面角的余弦值．

試題解析：

（1）取DC中點O，連接PO．

∵側(cè)面PDC是正三角形，

∴PO⊥DC，

又平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝DC，

∴PO⊥底面ABCD．

又底面ABCD為菱形，且∠ADC＝60°，DC＝2，

∴DO＝1，OA⊥DC．

以O為原點，分別以OA，OC，OP所在直線為x軸，y軸，z軸，建立如圖所示的空間直角坐標系O-xyz．

則， ，

∴，

∴，

∴PA⊥DM，PA⊥DC，

又DM∩DC＝D，

∴PA⊥平面CDM．

(2)由（1）得，

設(shè)平面BMC的一個法向量，

由，得，

令z＝1，得．

由(1)知平面CDM的法向量為，

∴，

由圖形知二面角D－MC－B是鈍角，

所以二面角D－MC－B的余弦值為．