
【題目】已知兩直線![]()
(1)求直線![]() 與
與![]() 的交點
的交點![]() 的坐標;
的坐標;
(2)求過![]() 交點
交點![]() ,且在兩坐標軸截距相等的直線方程;
,且在兩坐標軸截距相等的直線方程;
(3)若直線![]() 與
與![]() 不能構成三角形,求實數
不能構成三角形,求實數![]() 的值.
的值.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,調查數據表明,環境治理和保護問題仍是百姓最為關心的熱點,參與調查者中關注此問題的約占![]() .現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組
.現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(1)求出![]() 的值;
的值;
(2)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取5人,再從這5人中隨機抽取3人進行問卷調查,求第2組恰好抽到2人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:min)繪制了如下莖葉圖:
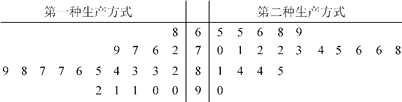
(1)根據莖葉圖判斷哪種生產方式的效率更高?并說明理由;
(2)求40名工人完成生產任務所需時間的中位數![]() ,并將完成生產任務所需時間超過
,并將完成生產任務所需時間超過![]() 和不超過
和不超過![]() 的工人數填入下面的列聯表:
的工人數填入下面的列聯表:
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
(3)根據(2)中的列聯表,能否有99%的把握認為兩種生產方式的效率有差異?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面凸四邊形![]() 中(凸四邊形指沒有角度數大于
中(凸四邊形指沒有角度數大于![]() 的四邊形),
的四邊形),![]() .
.
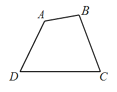
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)已知![]() ,記四邊形
,記四邊形![]() 的面積為
的面積為![]() .
.
① 求![]() 的最大值;
的最大值;
② 若對于常數![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.(直接寫結果,不需要過程)
的取值范圍.(直接寫結果,不需要過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大報告指出,建設生態文明是中華民族永續發展的千年大計.而清潔能源的廣泛使用將為生態文明建設提供更有力的支撐.沼氣作為取之不盡、用之不竭的生物清潔能源,在保護綠水青山方面具有獨特功效.通過辦沼氣帶來的農村“廁所革命”,對改善農村人居環境等方面,起到立竿見影的效果.為了積極響應國家推行的“廁所革命”,某農戶準備建造一個深為2米,容積為32立方米的長方體沼氣池,如果池底每平方米的造價為150元,池壁每平方米的造價為120元,沼氣池蓋子的造價為3000元,問怎樣設計沼氣池能使總造價最低?最低總造價是多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+1|. (I)求不等式f(x)<|2x+1|﹣1的解集M;
(Ⅱ)設a,b∈M,證明:f(ab)>f(a)﹣f(﹣b).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() 與直線
與直線![]() :
:![]() ,動直線
,動直線![]() 過定點
過定點![]() .
.

(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 兩點,點M是PQ的中點,直線
兩點,點M是PQ的中點,直線![]() 與直線
與直線![]() 相交于點N.探索
相交于點N.探索![]() 是否為定值,若是,求出該定值;若不是,請說明理由.
是否為定值,若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某觀光海域AB段的長度為3百公里,一超級快艇在AB段航行,經過多次試驗得到其每小時航行費用Q(單位:萬元)與速度v(單位:百公里/小時)(0≤v≤3)的以下數據:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
為描述該超級快艇每小時航行費用Q與速度v的關系,現有以下三種函數模型供選擇:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)試從中確定最符合實際的函數模型,并求出相應的函數解析式;
(2)該超級快艇應以多大速度航行才能使AB段的航行費用最少?并求出最少航行費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐E﹣ABCD中,底面ABCD為矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F為CE的中點,
(1)求證:AE∥平面BDF;
(2)求證:平面BDF⊥平面ACE;
(3)2AE=EB,在線段AE上找一點P,使得二面角P﹣DB﹣F的余弦值為![]() , 求AP的長.
, 求AP的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com