
【題目】已知橢圓![]() 過點
過點![]() ,且橢圓
,且橢圓![]() 的一個頂點
的一個頂點![]() 的坐標為
的坐標為![]() .過橢圓
.過橢圓![]() 的右焦點
的右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() (
(![]() ,
,![]() 不同于點
不同于點![]() ),直線
),直線![]() 與直線
與直線![]() :
:![]() 交于點
交于點![]() .連接
.連接![]() ,過點
,過點![]() 作
作![]() 的垂線與直線
的垂線與直線![]() 交于點
交于點![]() .
.
(1)求橢圓![]() 的方程,并求點
的方程,并求點![]() 的坐標;
的坐標;
(2)求證:![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
【答案】(1)![]() ,
,![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)根據題意列方程組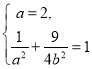 ,即可得到橢圓的方程,進而得到焦點坐標;
,即可得到橢圓的方程,進而得到焦點坐標;
(2)討論直線![]() 的斜率,利用
的斜率,利用![]() 是平行的證明
是平行的證明![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
(1) 因為點![]() 在橢圓
在橢圓![]() 上,且橢圓
上,且橢圓![]() 的一個頂點
的一個頂點![]() 的坐標為
的坐標為![]() ,
,
所以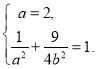 解得
解得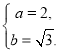
所以橢圓![]() 的方程為
的方程為![]() .
.
所以橢圓![]() 的右焦點
的右焦點![]() 的坐標為
的坐標為![]() .
.
(2)① 當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]() .
.
顯然,![]() ,
,![]() 或
或![]() ,
,![]() .
.
當![]() ,
,![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
所以![]() .
.
直線![]() 的方程為
的方程為![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
則![]() ,
,![]() .
.
所以![]() ,所以
,所以![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
同理,當![]() ,
,![]() 時,
時,![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
② 當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() .
.
由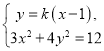 得
得![]() .
.
且![]() .
.
設![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
直線![]() 的方程為
的方程為![]() ,點
,點![]() 的坐標為
的坐標為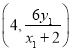 .
.
所以 .
.
直線![]() 的方程為
的方程為![]() ,點
,點![]() 的坐標為
的坐標為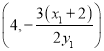 .
.
則![]() ,
,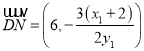 .
.
所以![]()
![]() ,
,
![]() ,
,
![]() ,
,
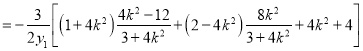 ,
,
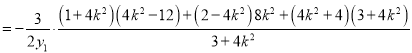 ,
,
![]()
![]() .
.
所以![]() 與
與![]() 共線,
共線,
所以![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
綜上所述,![]() ,
,![]() ,
,![]() 三點共線.
三點共線.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,經過點
,經過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:對于任意![]() ,滿足條件
,滿足條件![]() 且
且![]() (M是與n無關的常數)的無窮數列
(M是與n無關的常數)的無窮數列![]() 稱為M數列.
稱為M數列.
(1)若等差數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,判斷數列
,判斷數列![]() 是否是M數列,并說明理由;
是否是M數列,并說明理由;
(2)若各項為正數的等比數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,證明:數列
,證明:數列![]() 是M數列,并指出M的取值范圍;
是M數列,并指出M的取值范圍;
(3)設數列![]() ,問數列
,問數列![]() 是否是M數列?請說明理由.
是否是M數列?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:{an}是公比大于1的等比數列,Sn為其前n項和,S3=7,且a1+3,3a2,a3+4構成等差數列.
(1)求數列{an}的通項公式;
(2)令bn=log2a3n+1,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求![]() 在區間
在區間![]() 上的最大值和最小值;
上的最大值和最小值;
(2)在曲線![]() 上是否存在點P,使得過點P可作三條直線與曲線
上是否存在點P,使得過點P可作三條直線與曲線![]() 相切?若存在,求出其橫坐標的取值范圍;若不存在,請說明理由.
相切?若存在,求出其橫坐標的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學經典《九章算術》系統地總結了戰國、秦、漢時期的數學成就,書中將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的三棱錐稱之為鱉臑,如圖為一個陽馬與一個鱉臑的組合體,已知![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,
為正方形,![]() ,
,![]() ,若鱉臑
,若鱉臑![]() 的外接球的體積為
的外接球的體積為![]() ,則陽馬
,則陽馬![]() 的外接球的表面積等于______.
的外接球的表面積等于______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某校運動會男生組田徑綜合賽以選手三項運動的綜合積分高低決定排名.具體積分規則如表1所示,某代表隊四名男生的模擬成績如表2.
表1 田徑綜合賽項目及積分規則
項目 | 積分規則 |
| 以 |
跳高 | 以 |
擲實心球 | 以 |
表2 某隊模擬成績明細
姓名 | 100米跑(秒) | 跳高(米) | 擲實心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根據模擬成績,該代表隊應選派參賽的隊員是:( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com