
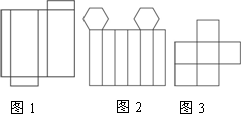
圖1、圖2、圖3中的幾個圖形能否折疊成棱柱?請試折一下并回答為什么.
|
答案:圖1可折成一個四棱柱;圖2不能折成棱柱,因為折成后的幾何體兩底面在同一平面內;圖3不能折成棱柱,因為與正方體的每個面相鄰的面最多只有四個,因而展開后的圖形中,任一個正方形在它的周圍最多只應有四個正方形,而圖中有一個正方形,在它的周圍有5個正方形,這是不可能的. 思路解析:首先判斷各圖如果能折成棱柱則應該折成什么樣的棱柱,再看各圖與相應棱柱展開圖有什么差異.這個題主要要求學生把握多面體的基本情況,運用紙張折疊,結合想象,掌握簡單幾何體的性質與構成. |
|
我們常見的多面體如棱柱、棱錐和棱臺等,均可展開成平面圖形,反之滿足一定條件的平面圖形亦可還原成空間多面體.在剛接觸有關立體幾何的內容時,一定要養成多動手、勤觀察、善思考、好總結的良好習慣,為進一步學習立體幾何的知識打下堅實的基礎. |


科目:高中數學 來源:設計必修二數學蘇教版 蘇教版 題型:013
圖1、圖2、圖3中的圖形折疊后的圖形分別是
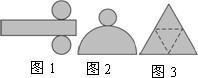
A.圓柱、圓錐、棱柱
B.圓柱、圓錐、棱錐
C.圓臺、球棱錐
D.圓臺、圓錐、棱柱
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com