
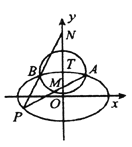
【題目】如圖,橢圓![]() 的離心率為
的離心率為![]() ,以橢圓
,以橢圓![]() 的上頂點
的上頂點![]() 為圓心作圓,
為圓心作圓,
![]() ,圓
,圓![]() 與橢圓
與橢圓![]() 在第一象限交于點
在第一象限交于點![]() ,在第二象限交于點
,在第二象限交于點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此時圓
的最小值,并求出此時圓![]() 的方程;
的方程;
(3)設(shè)點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的一點,且直線
的一點,且直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() 為坐標(biāo)原點,求證:
為坐標(biāo)原點,求證:
![]() 為定值.
為定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】試題分析:(1)依據(jù)題設(shè)條件求出參數(shù)即可;(2)依據(jù)題設(shè)條件及向量的數(shù)量積公式建立目標(biāo)函數(shù),再借助該函數(shù)取得最小值時求出圓的方程;(3)借助直線與橢圓的位置關(guān)系進(jìn)行分析推證:
試題解析:
(1) 由題意知, ![]() ,得
,得![]() .
.
故橢圓![]() 的方程為
的方程為![]() .
.
(2) ![]() 點
點![]() 與點
與點![]() 關(guān)于
關(guān)于![]() 軸對稱,設(shè)
軸對稱,設(shè)![]() ,由點
,由點![]() 橢圓
橢圓![]() 上,則
上,則![]() ,得
,得![]()
![]() .由題意知,
.由題意知, ![]() ,
,![]() 當(dāng)
當(dāng)![]() 時,
時, ![]() 取得最小值
取得最小值![]() .此時,
.此時, ![]() ,故
,故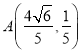 .又點
.又點![]() 在圓
在圓![]() 上,代入圓的方程,得
上,代入圓的方程,得![]() .
.
故圓![]() 的方程為
的方程為![]() .
.
(3)設(shè)![]() ,則
,則![]() 的方程為
的方程為![]() .令
.令![]() ,得
,得![]() .同理可得,
.同理可得, ![]() . 故
. 故![]() . ①
. ①
![]() 都在橢圓
都在橢圓![]() 上,
上, ![]() ,代入①得,
,代入①得, 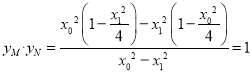 .即得
.即得![]() 為定值.
為定值.


 一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
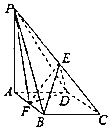
【題目】如圖:在四棱錐P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E是PC中點,F是AB中點.
(Ⅰ)求證:BE∥平面PDF;
(Ⅱ)求直線PD與平面PFB所成角的正切值;
(Ⅲ)求三棱錐P﹣DEF的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)已知拋物線![]() 的頂點在坐標(biāo)原點
的頂點在坐標(biāo)原點![]() ,對稱軸為
,對稱軸為![]() 軸,焦點為
軸,焦點為![]() ,拋物線上一點
,拋物線上一點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,且
,且![]() .
.
(Ⅰ)求此拋物線![]() 的方程;
的方程;
(Ⅱ)過點![]() 做直線
做直線![]() 交拋物線
交拋物線![]() 于
于![]() 兩點,求證:
兩點,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】輪船![]() 從某港口將一些物品送到正航行的輪船
從某港口將一些物品送到正航行的輪船![]() 上,在輪船
上,在輪船![]() 出發(fā)時,輪船
出發(fā)時,輪船![]() 位于港口
位于港口![]() 北偏西
北偏西![]() 且與
且與![]() 相距20海里的
相距20海里的![]() 處,并正以30海里的航速沿正東方向勻速行駛,假設(shè)輪船
處,并正以30海里的航速沿正東方向勻速行駛,假設(shè)輪船![]() 沿直線方向以
沿直線方向以![]() 海里/小時的航速勻速行駛,經(jīng)過
海里/小時的航速勻速行駛,經(jīng)過![]() 小時與輪船
小時與輪船![]() 相遇.
相遇.
(1)若使相遇時輪船![]() 航距最短,則輪船
航距最短,則輪船![]() 的航行速度大小應(yīng)為多少?
的航行速度大小應(yīng)為多少?
(2)假設(shè)輪船![]() 的最高航速只能達(dá)到30海里/小時,則輪船
的最高航速只能達(dá)到30海里/小時,則輪船![]() 以多大速度及什么航行方向才能在最短時間與輪船
以多大速度及什么航行方向才能在最短時間與輪船![]() 相遇,并說明理由.
相遇,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某大理石工廠初期花費98萬元購買磨大理石刀具,第一年需要各種費用12萬元,從第二年起,每年所需費用比上一年增加4萬元,該大理石加工廠每年總收入50萬元.
(1)到第幾年末總利潤最大,最大值是多少?
(2)到第幾年末年平均利潤最大,最大值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓心為![]() 的圓過點
的圓過點![]() 和
和![]() ,且圓心在直線
,且圓心在直線![]() :
: ![]() 上.
上.
(1)求圓心為![]() 的圓的標(biāo)準(zhǔn)方程;
的圓的標(biāo)準(zhǔn)方程;
(2)過點 ![]() 作圓的切線,求切線方程.
作圓的切線,求切線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在[﹣1,1]上的奇函數(shù)f(x),已知當(dāng)x∈[﹣1,0]時的解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)寫出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 與圓
與圓![]()
(1)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩個不同點,求
兩個不同點,求![]() 的最小值;
的最小值;
(2)直線![]() 上是否存在點
上是否存在點![]() ,滿足經(jīng)過點
,滿足經(jīng)過點![]() 有無數(shù)對互相垂直的直線
有無數(shù)對互相垂直的直線![]() 和
和![]() ,它們分別與圓
,它們分別與圓![]() 和圓
和圓![]() 相交,并且直線
相交,并且直線![]() 被圓
被圓![]() 所截得的弦長等于直線
所截得的弦長等于直線![]() 被圓
被圓![]() 所截得的弦長?若存在,求出點
所截得的弦長?若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某廠擬生產(chǎn)甲、乙兩種適銷產(chǎn)品,每件銷售收入分別為3萬元、2萬元,甲、乙產(chǎn)品都需要在![]() 兩種設(shè)備上加工,在每臺
兩種設(shè)備上加工,在每臺![]() 上加工1件甲所需工時分別是1
上加工1件甲所需工時分別是1![]() 、2
、2![]() ,加工1件乙所需工時分別為2
,加工1件乙所需工時分別為2![]() 、1
、1![]() ,
, ![]() 兩種設(shè)備每月有效使用臺時數(shù)分別為400
兩種設(shè)備每月有效使用臺時數(shù)分別為400![]() 和500
和500![]() ,如何安排生產(chǎn)可使收入最大?
,如何安排生產(chǎn)可使收入最大?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com