
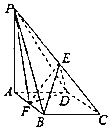
【題目】如圖:在四棱錐P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E是PC中點,F是AB中點.
(Ⅰ)求證:BE∥平面PDF;
(Ⅱ)求直線PD與平面PFB所成角的正切值;
(Ⅲ)求三棱錐P﹣DEF的體積.
【答案】(Ⅰ)見解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】試題解析:(Ⅰ)利用三角形的中位線定理、平行四邊形的判定與性質定理及線面平行的判定定理即可證明取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,則可證四邊形
,則可證四邊形![]() 是平行四邊形,得出
是平行四邊形,得出![]() ,從而證明結論;(Ⅱ)先證
,從而證明結論;(Ⅱ)先證![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,利用線面垂直的性質定理可證明
,利用線面垂直的性質定理可證明![]() ⊥平面
⊥平面![]() 可得∠
可得∠![]() 為直線
為直線![]() 與平面
與平面![]() 所成角,利用直角三角形選擇求求其正切值,即可得結果;(Ⅲ)利用等積變形和三棱錐的體積計算公式可得
所成角,利用直角三角形選擇求求其正切值,即可得結果;(Ⅲ)利用等積變形和三棱錐的體積計算公式可得![]() =
=![]() =
=![]() .
.
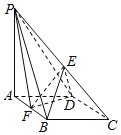
(Ⅰ)證明:取![]() 中點
中點![]() ,連
,連![]() ,
,![]() ;
;
因為![]() ,
,![]() 分別為
分別為![]() ,
, ![]() 中點,所以
中點,所以![]() ,
, ![]() ∥
∥![]() ;
;
且![]() 是
是![]() 中點,
中點, ![]() ,
, ![]() ∥
∥![]() ;
;
且![]() ∥
∥![]() ,
,
則四邊形![]() 為平行四邊形
為平行四邊形
所以![]() ∥
∥![]() ,且
,且![]()
![]() 平面
平面![]() ;
; ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)解:因為![]() ⊥底面
⊥底面![]() ,
, ![]()
![]() 底面
底面![]() ,所以
,所以![]() ⊥
⊥![]() ;
;
又因為底面![]() 是菱形,
是菱形, ![]() =2,
=2, ![]() =1,∠
=1,∠![]() =
=![]() ,則
,則![]() ,
,
![]()
![]() +
+ ![]()
![]() =
= ![]()
![]() ,
, ![]() ⊥
⊥![]() ,
,
且![]() , 所以
, 所以![]() ⊥平面
⊥平面![]() ,
,
則![]() 是
是![]() 在平面
在平面![]() 內的射影,
內的射影,
∠![]() 為直線
為直線![]() 與平面
與平面![]() 所成角,
所成角,
![]() =
=![]() =
=![]()
(Ⅲ)解:因為![]() 是
是![]() 中點,點
中點,點![]() 到平面
到平面![]() 的距離等于點
的距離等于點![]() 到平面
到平面![]() 的距離,
的距離,
![]() =
=![]() =
=![]() .
.
【方法點晴】本題主要考查線面平行的判定定理、直線和平面成的角的定義及求法、利用等積變換求三棱錐體積,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質,即兩平面平行,在其中一平面內的直線平行于另一平面. 本題(1)是就是利用方法①證明的.


科目:高中數學 來源: 題型:
【題目】某研究所計劃利用“神七”宇宙飛船進行新產品搭載實驗,計劃搭載新產品![]() 、
、![]() ,該所要根據該產品的研制成本、產品重量、搭載實驗費用、和預計產生收益來決定具體安排.通過調查,有關數據如下表:
,該所要根據該產品的研制成本、產品重量、搭載實驗費用、和預計產生收益來決定具體安排.通過調查,有關數據如下表:
產品A(件) | 產品B(件) | ||
研制成本、搭載費用之和(萬元) | 20 | 30 | 計劃最大資金額300萬元 |
產品重量(千克) | 10 | 5 | 最大搭載重量110千克 |
預計收益(萬元) | 80 | 60 |
如何安排這兩種產品的件數進行搭載,才能使總預計收益達到最大,最大收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,已知中心在原點,焦點在x軸上的雙曲線C的離心率為![]() ,且雙曲線C與斜率為2的直線l相交,且其中一個交點為P(﹣3,0).
,且雙曲線C與斜率為2的直線l相交,且其中一個交點為P(﹣3,0).
(1)求雙曲線C的方程及它的漸近線方程;
(2)求以直線l與坐標軸的交點為焦點的拋物線的標準方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種商品在30天內每件的銷售價格P(元)與時間t(天)的函數關系用下圖的兩條線段表示;該商品在30天內日銷售量Q(件)與時間t(天)之間的關系Q=﹣t+40. 
(1)根據提供的圖象,寫出該商品每件的銷售價格P與時間t的函數關系式;
(2)問這30天內,哪天的銷售額最大,最大是多少?(銷售額=銷售價格×銷售量)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】血藥濃度(Plasma Concentration)是指藥物吸收后在血漿內的總濃度. 藥物在人體內發揮治療作用時,該藥物的血藥濃度應介于最低有效濃度和最低中毒濃度之間.已知成人單次服用1單位某藥物后,體內血藥濃度及相關信息如圖所示:
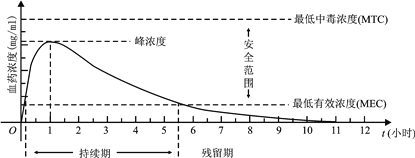
根據圖中提供的信息,下列關于成人使用該藥物的說法中,不正確的個數是
①首次服用該藥物1單位約10分鐘后,藥物發揮治療作用
②每次服用該藥物1單位,兩次服藥間隔小于2小時,一定會產生藥物中毒
③每間隔5.5小時服用該藥物1單位,可使藥物持續發揮治療作用
④首次服用該藥物1單位3小時后,再次服用該藥物1單位,不會發生藥物中毒
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一系列函數的解析式和值域相同,但是定義域不同,則稱這些函數為“同族函數”,例如函數y=x2 , x∈[1,2],與函數y=x2 , x∈[﹣2,﹣1]即為“同族函數”.下面的函數解析式也能夠被用來構造“同族函數”的是( )
A.y=x
B.y=|x﹣3|
C.y=2x
D.y=log ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
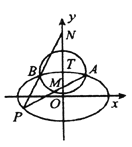
【題目】如圖,橢圓![]() 的離心率為
的離心率為![]() ,以橢圓
,以橢圓![]() 的上頂點
的上頂點![]() 為圓心作圓,
為圓心作圓,
![]() ,圓
,圓![]() 與橢圓
與橢圓![]() 在第一象限交于點
在第一象限交于點![]() ,在第二象限交于點
,在第二象限交于點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的最小值,并求出此時圓
的最小值,并求出此時圓![]() 的方程;
的方程;
(3)設點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的一點,且直線
的一點,且直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() 為坐標原點,求證:
為坐標原點,求證:
![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com