
【題目】已知函數(shù)![]() .
.
(1)求![]() 的極大值點;
的極大值點;
(2)當(dāng)![]() ,
,![]() 時,若過點
時,若過點![]() 存在3條直線與曲線
存在3條直線與曲線![]() 相切,求t的取值范圍.
相切,求t的取值范圍.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)先求導(dǎo)數(shù),求出導(dǎo)函數(shù)的零點,安照![]() 、
、![]() 、
、![]() 三種情況討論
三種情況討論![]() 的極大值點;
的極大值點;
(2)設(shè)切點![]() ,利用該點的導(dǎo)數(shù)等于切線斜率、切線過點
,利用該點的導(dǎo)數(shù)等于切線斜率、切線過點![]() 兩個條件整理得到關(guān)于
兩個條件整理得到關(guān)于![]() 的方程
的方程![]() ,進(jìn)一步研究函數(shù)
,進(jìn)一步研究函數(shù)![]() 的取值情況.
的取值情況.
解:(1)![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
若![]() ,則當(dāng)
,則當(dāng)![]() 時,
時,![]() ;
;
當(dāng)![]() 時,
時,![]() ,
,
故![]() 在
在![]() ,
,![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
此時![]() 的極大值點為
的極大值點為![]() ;
;
若![]() ,則當(dāng)
,則當(dāng)![]() 時,
時,![]() ;
;
當(dāng)![]() 時,
時,![]() ,
,
故![]() 在
在![]() ,
,![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
此時![]() 的極大值點為
的極大值點為![]() ;
;
若![]() ,
,![]() 在
在![]() 上單調(diào)遞增,無極值.
上單調(diào)遞增,無極值.
(2)設(shè)過點![]() 的直線與曲線
的直線與曲線![]() 相切于點
相切于點![]() ,
,
則![]() ,且切線斜率
,且切線斜率![]() ,
,
所以切線方程為![]() ,
,
因此![]() ,整理得
,整理得![]() ,
,
構(gòu)造函數(shù)![]() ,
,
則“若過點![]() 存在3條直線與曲線
存在3條直線與曲線![]() 相切”等價于“
相切”等價于“![]() 有三個不同的零點”,
有三個不同的零點”,![]() ,
,![]() 與
與![]() 的關(guān)系如下表:
的關(guān)系如下表:
|
|
|
|
|
|
| + | 0 | 0 | + | |
|
| 極大值 |
| 極小值 |
|
所以![]() 的極大值為
的極大值為![]() ,極小值為
,極小值為![]() ,
,
要使![]() 有三個解,即
有三個解,即![]() 且
且![]() ,解得
,解得![]() .
.
因此,當(dāng)過點![]() 存在3條直線與曲線
存在3條直線與曲線![]() 相切時,
相切時,
t的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 為等邊三角形,且垂直于底面
為等邊三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)已知點![]() 在棱
在棱![]() 上且
上且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠在制造產(chǎn)品時需要用到長度為698mm的A型和長度為518mm的B型兩種鋼管,工廠利用長度為4000mm的鋼管原材料,裁剪成若干A型和B型鋼管。假設(shè)裁剪時損耗忽略不計,裁剪后所剩廢料與原材料的百分比稱為廢料率.
(1)有兩種裁剪方案的廢料率小于4.5%,請說明這兩種方案并計算它們的廢料率;
(2)工廠現(xiàn)有100根原材料鋼管,一根A型和一根B型鋼管為一套毛胚。按(1)中的方案裁剪,最多可裁剪多少套毛胚?最終的廢料率為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】當(dāng)今世界科技迅猛發(fā)展,信息日新月異.為增強全民科技意識,提高公眾科學(xué)素養(yǎng),某市圖書館開展了以“親近科技、暢想未來”為主題的系列活動,并對不同年齡借閱者對科技類圖書的情況進(jìn)行了調(diào)查.該圖書館從只借閱了一本圖書的借閱者中隨機抽取100名,數(shù)據(jù)統(tǒng)計如表:
借閱科技類圖書(人) | 借閱非科技類圖書(人) | |
年齡不超過50歲 | 20 | 25 |
年齡大于50歲 | 10 | 45 |
(1)是否有99%的把握認(rèn)為年齡與借閱科技類圖書有關(guān)?
(2)該圖書館為了鼓勵市民借閱科技類圖書,規(guī)定市民每借閱一本科技類圖書獎勵積分2分,每借閱一本非科技類圖書獎勵積分1分,積分累計一定數(shù)量可以用積分換購自己喜愛的圖書.用表中的樣本頻率作為概率的估計值.
(i)現(xiàn)有3名借閱者每人借閱一本圖書,記此3人增加的積分總和為隨機變量ξ,求ξ的分布列和數(shù)學(xué)期望;
(ii)現(xiàn)從只借閱一本圖書的借閱者中選取16人,則借閱科技類圖書最有可能的人數(shù)是多少?
附:K2![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,E,F分別為
,E,F分別為![]() ,
,![]() 邊的中點.現(xiàn)將
邊的中點.現(xiàn)將![]() 沿著
沿著![]() 折疊到
折疊到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() .
.
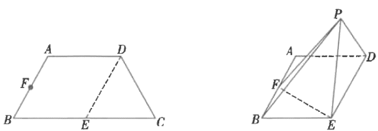
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】元朝著名的數(shù)學(xué)家朱世杰在《四元玉鑒》中有一首詩:“我有一壺酒,攜著游春走.遇店添一倍,逢友飲一斗.”基于此情景,設(shè)計了如圖所示的程序框圖,若輸入的![]() ,輸出的
,輸出的![]() ,則判斷框中可以填( )
,則判斷框中可以填( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平面直角坐標(biāo)系![]() 中,已知點
中,已知點![]() ,直線
,直線![]() ,動點
,動點![]() 到點
到點![]() 的距離比它到直線
的距離比它到直線![]() 的距離小2.
的距離小2.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設(shè)斜率為2的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點(點
兩點(點![]() 在第一象限),過點
在第一象限),過點![]() 作
作![]() 軸的平行線
軸的平行線![]() ,問在坐標(biāo)平面
,問在坐標(biāo)平面![]() 中是否存在定點
中是否存在定點![]() ,使直線
,使直線![]() 交直線
交直線![]() 于點
于點![]() ,且
,且![]() 恒成立?若存在,求出點
恒成立?若存在,求出點![]() 的坐標(biāo),若不存在,說明理由.
的坐標(biāo),若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|x+1|﹣|2x﹣2|的最大值為M,正實數(shù)a,b滿足a+b=M.
(1)求2a2+b2的最小值;
(2)求證:aabb≥ab.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com