已知平面
∥
，在內(nèi)有4個點，在內(nèi)有6個點.
（1）過這10個點中的3點作一平面，最多可作多少個不同平面？
（2）以這些點為頂點，最多可作多少個三棱錐？
（3）上述三棱錐中最多可以有多少個不同的體積？
(1)98 (2)194 (3)114
（1）所作出的平面有三類：①
內(nèi)1點，
內(nèi)2點確定的平面，有C
·C
個；②內(nèi)2點，內(nèi)1點確定的平面，有C
·C
個；③，本身.
∴所作的平面最多有C·C+C·C+2=98（個）.
（2）所作的三棱錐有三類：①內(nèi)1點，內(nèi)3點確定的三棱錐，有C·C
個；②內(nèi)2點，內(nèi)2點確定的三棱錐，有C·C個；內(nèi)3點，內(nèi)1點確定的三棱錐，有C
·C個.
∴最多可作出的三棱錐有：C·C+C·C+C·C=194（個）.
（3）∵當?shù)鹊酌娣e、等高的情況下三棱錐的體積相等,
且平面∥，∴體積不相同的三棱錐最多有
C+C+C·C=114（個）.
科目：高中數(shù)學 來源：2010年普通高等學校招生全國統(tǒng)一考試（重慶卷）數(shù)學理工類模擬試卷（四） 題型：填空題
已知平面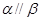
，在
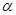內(nèi)有4個點，在
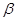內(nèi)有6個點，以這些點為頂點，最多可作 個三棱錐，在這些三棱錐中最多可以有 個不同的體積．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
（12分）已知平面
∥
，在平面內(nèi)有4個點，在內(nèi)有6個點
(1) 過這10個點中的3個點作一個平面，最多可以作多少個不同的平面；
(2) 以這些點為頂點，最多可作多少個三棱錐；
(3) 上述三棱錐中最多可以有多少個不同的體積；
(4) 在經(jīng)過每兩點的連線中，最多有多少對異面直線。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com