
【題目】已知函數![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)是否存在實數a,使函數![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() ,若存在,求出a的值,若不存在,請說明理由.
,若存在,求出a的值,若不存在,請說明理由.
 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() (b為常數)
(b為常數)
(1)若b=1,求函數H(x)=f(x)﹣g(x)圖象在x=1處的切線方程;
(2)若b≥2,對任意x1,x2∈[1,2],且x1≠x2,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求實數b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如題所示的平面圖形中,![]() 為矩形,
為矩形,![]() ,
,![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 是以
是以![]() 為圓心,
為圓心,![]() 為直徑的半圓上任一點(不與
為直徑的半圓上任一點(不與![]() 重合),以
重合),以![]() 為折痕,將半圓所在平面
為折痕,將半圓所在平面![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如圖2,
,如圖2,![]() 為線段
為線段![]() 的中點.
的中點.
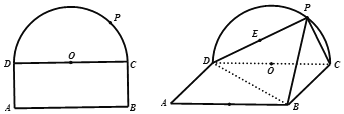
(1)證明:![]() .
.
(2)若銳二面角![]() 的大小為
的大小為![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1所示,在等腰梯形ABCD中,![]() ,
,![]() ,垂足為E,
,垂足為E,![]() ,
,![]() 將
將![]() 沿EC折起到
沿EC折起到![]() 的位置,如圖2所示,使平面
的位置,如圖2所示,使平面![]() 平面ABCE.
平面ABCE.
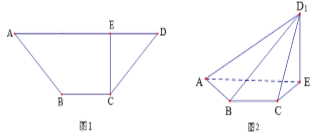
(1)連結BE,證明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點G,使得
上是否存在點G,使得![]() 平面
平面![]() ,若存在,直接指出點G的位置
,若存在,直接指出點G的位置![]() 不必說明理由
不必說明理由![]() ,并求出此時三棱錐
,并求出此時三棱錐![]() 的體積;若不存在,請說明理由.
的體積;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com