【題目】某工廠擬修建一個無蓋的圓柱形蓄水池（不計厚度）.設該蓄水池的底面半徑為
米，高為
米，體積為
立方米.假設建造成本僅與表面積有關，側面的建造成本為100元/平方米，底面的建造成本為160元/平方米，該蓄水池的總建造成本為
元（
為圓周率）.該蓄水池的體積最大時
______.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】《張丘建算經》是中國古代的著名數學著作，該書表明：至遲于公元5世紀，中國已經系統掌握等差數列的相關理論，該書上卷22題又“女工善織問題”：“今有女善織，日益功疾，初日織五尺，今一月曰織九匹三丈，問日益幾何？”，大概意思是：有一個女工人善于織布，每天織布的尺數越來越多且成等差數列，第一天知5尺，30天共織九匹三丈，問每天增加的織布數目是多少寸？答案是__________寸．（注：當時一匹為四丈，一丈為十尺，一尺為十寸，結果四舍五入精確到寸）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】坐標系與參數方程：在平面直角坐標系中，以原點
為極點，
軸的非負半軸為極軸建立極坐標系，已知點
的極坐標為
，直線
的極坐標方程為
，且點在直線上
（Ⅰ）求
的值和直線的直角坐標方程及的參數方程；
（Ⅱ）已知曲線
的參數方程為
，（
為參數），直線與交于
兩點，求
的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正三棱柱
的所有棱長都為
，
是
的中點，
在
邊上，
.
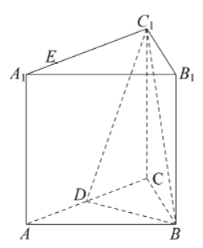
（1）證明：平面
平面
；
（2）若
是側面
內的動點，且
平面
.
①在答題卡中作出點的軌跡，并說明軌跡的形狀（不需要說明理由）；
②求三棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P﹣ABCD中，△PAB是邊長為2的等邊三角形，底面ABCD為直角梯形，AB∥CD，AB⊥BC，BC＝CD＝1，PD
.
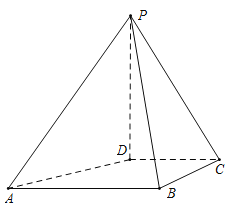
（1）證明：AB⊥PD.
（2）求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場一年中各月份的收入、支出情況的統計如圖所示，下列說法中正確的是______.
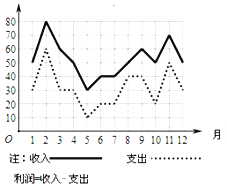
①2至3月份的收入的變化率與11至12月份的收入的變化率相同；
②支出最高值與支出最低值的比是6:1；
③第三季度平均收入為50萬元；
④利潤最高的月份是2月份。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，在四邊形
中，
，
，
，
.把
沿著
翻折至
的位置，
平面
，連結
，如圖2.
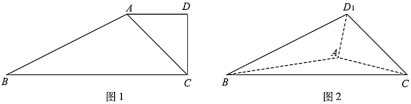
（1）當
時，證明：平面
平面
；
（2）當三棱錐
的體積最大時，求點
到平面
的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
