【題目】對以下命題：
①隨機事件的概率與頻率一樣，與試驗重復的次數有關；
②拋擲兩枚均勻硬幣一次，出現一正一反的概率是
；
③若一種彩票買一張中獎的概率是
，則買這種彩票一千張就會中獎；
④“姚明投籃一次，求投中的概率”屬于古典概型概率問題．
其中正確的個數是（ ）
A.0B.1C.2D.3
課課優能力培優100分系列答案
優百分課時互動系列答案科目：高中數學 來源： 題型：
【題目】坐標系與參數方程在平面直角坐標系
中，曲線
的參數方程為
（
為參數）.以坐標原點為極點，
軸的非負半軸為極軸且取相同的單位長度建立極坐標系，直線
的極坐標方程為
（
）.
（1）寫出直線的直角坐標方程與曲線的普通方程；
（2）平移直線使其經過曲線的焦點，求平移后的直線的極坐標方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著生活水平的提高，人們的休閑方式也發生了變化．某機構隨機調查了
個人，其中男性占調查人數的
．已知男性中有一半的人的休閑方式是運動，而女性只有
人的休閑方式是運動．
（1）完成下列
列聯表：
運動 | 非運動 | 總計 | |
男性 | |||
女性 | |||
總計 | n |
（2）若在犯錯誤的概率不超過
的前提下，可認為“性別與休閑方式有關”， 那么本次被調查的人數至少有多少？
（3）根據（2）的結論，本次被調查的人中，至少有多少人的休閑方式是運動？
參考公式
，其中
．
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司代理銷售某種品牌小商品，該產品進價為5元/件，銷售時還需交納品牌使用費3元/件，售價為
元/件，其中
，且
．根據市場調查，當
，且時，每月的銷售量
（萬件）與
成正比；當
，且
時，每月的銷售量（萬件）與
成反比．已知售價為15元/件時，月銷售量為9萬件．
（1）求該公司的月利潤
（萬件）與每件產品的售價（元）的函數關系式；
（2）當每件產品的售價為多少元時，該公司的月利潤最大？并求出最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
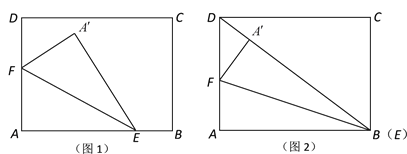
【題目】南通風箏是江蘇傳統手工藝品之一．現用一張長2 m，寬1.5 m的長方形牛皮紙ABCD裁剪風箏面，裁剪方法如下：分別在邊AB，AD上取點E，F，將三角形AEF沿直線EF翻折到
處，點
落在牛皮紙上，沿
，
裁剪并展開，得到風箏面
，如圖1．
（1）若點E恰好與點B重合，且點在BD上，如圖2，求風箏面
的面積；
（2）當風箏面的面積為
時，求點到AB距離的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為評估設備
生產某種零件的性能，從設備生產該零件的流水線上隨機抽取100個零件為樣本，測量其直徑后，整理得到下表：
直徑/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直徑/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算，樣本的平均值
，標準差
，以頻率值作為概率的估計值.
（I）為評判一臺設備的性能，從該設備加工的零件中任意抽取一件，記其直徑為
，并根據以下不等式進行判定（
表示相應事件的概率）：①
；②
；③
.判定規則為：若同時滿足上述三個式子，則設備等級為甲；若僅滿足其中兩個，則等級為乙；若僅滿足其中一個，則等級為丙；若全部都不滿足，則等級為丁.試判斷設備的性能等級.
（Ⅱ）將直徑尺寸在
之外的零件認定為是“次品”，將直徑尺寸在
之外的零件認定為“突變品”.從樣本的“次品”中隨意抽取兩件，求至少有一件“突變品”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在以
，
，
，
，
，
為頂點的五面體中，平面
平面
，
是邊長為
的正三角形，直線
與平面
所成角為
.
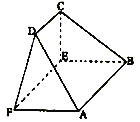
（I）求證：
；
（Ⅱ）若
，四邊形為平行四邊形，求平面
與平面
所成銳二面角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖①，利用斜二側畫法得到水平放置的
的直觀圖
，其中
軸，
軸.若
，設的面積為
，的面積為
，記
，執行如圖②的框圖，則輸出
的值
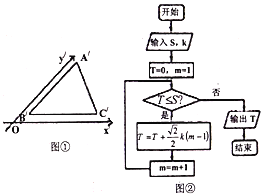
A. 12B. 10C. 9D. 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
