
已知拋物線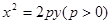 過點
過點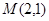 .
.
(I)求拋物線的方程;
(II)已知圓心在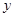 軸上的圓
軸上的圓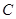 過點
過點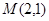 ,且圓
,且圓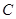 在點
在點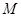 的切線恰是拋物線在點
的切線恰是拋物線在點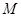 的切線,求圓
的切線,求圓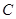 的方程;
的方程;
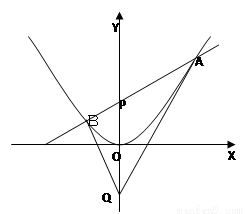
(Ⅲ)如圖,點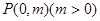 為
為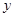 軸上一點,點
軸上一點,點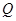 是點
是點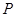 關于原點的對稱點,過點
關于原點的對稱點,過點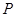 作一條直線與拋物線交于
作一條直線與拋物線交于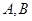 兩點,若
兩點,若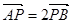 ,證明:
,證明: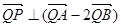 .
.
(I)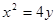 ;(II)
;(II)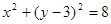 ;(Ⅲ)見解析。
;(Ⅲ)見解析。
【解析】
試題分析:(I)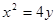
(II)由 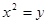 得
得 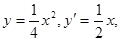 所以拋物線
所以拋物線
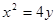 在點
在點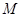 處切線的斜率為
處切線的斜率為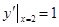
 過點
過點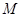 且與切線垂直的直線方程為:
且與切線垂直的直線方程為: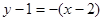 ,即
,即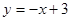 ,令
,令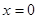 得
得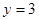
 圓心
圓心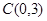 ,半徑
,半徑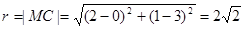
圓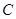 的方程為:
的方程為: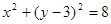
(Ⅲ)設直線AB的方程為 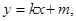 代入拋物線方程
代入拋物線方程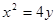 得
得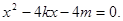
設A、B兩點的坐標分別是
 、
、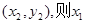 、x2是方程①的兩根.
、x2是方程①的兩根.
所以 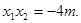 ①
①
由 得
得
 即
即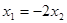 ②
②
由①、②可得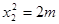
又點Q是點P關于原點的對稱點,故點Q的坐標是(0,-m),從而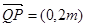 .
.
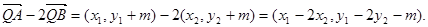
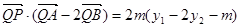
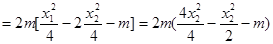
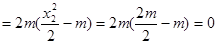
所以 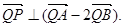
考點:拋物線的簡單性質;圓的簡單性質;導數的幾何意義;直線與拋物線的綜合應用。
點評::研究直線與拋物線的綜合問題,通常的思路是:轉化為研究方程組的解的問題,利用直線方程與拋物線方程所組成的方程組消去一個變量后,將交點問題(包括公共點個數、與交點坐標有關的問題)轉化為一元二次方程根的問題,結合根與系數的關系及判別式解決問題。


科目:高中數學 來源:四川省成都外國語學院高三2010-2011學年9月月考數學試題(理科) 題型:選擇題
已知拋物線過點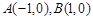 ,且以圓
,且以圓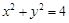 的切線為準線,則拋物線的焦點的軌跡方程為( )
的切線為準線,則拋物線的焦點的軌跡方程為( )
A.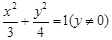 B.
B.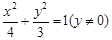 C.
C.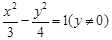 D.
D.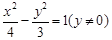
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com