Question

【題目】數列{bn}（bn＞0）的首項為1，且前n項和Sn滿足Sn﹣Sn﹣1= + （n≥2）．
（1）求{bn}的通項公式；
（2）若數列{ }前n項和為Tn ， 問Tn＞ 的最小正整數n是多少？

Answer 1

【答案】
（1）解：∵數列{bn}（bn＞0）的首項為1，前n項和Sn滿足Sn﹣Sn﹣1= + （n≥2）．

∴ ﹣ =1，∴數列 構成一個首相為1公差為1的等差數列，

∴ =1+（n﹣1）×1=n，∴Sn=n2．

∴n≥2時，bn=Sn﹣Sn﹣1=n2﹣（n﹣1）2=2n﹣1．（n=1時也成立）．

∴bn=2n﹣1．

（2）解： = = ．

∴數列{ }前n項和Tn= +…+ = = ．

Tn＞ 即： ＞ ，解得n＞ ．

滿足Tn＞ 的最小正整數為112

【解析】（1）數列{bn}（bn＞0）的首項為1，前n項和Sn滿足Sn﹣Sn﹣1= + （n≥2）．可得 ﹣ =1，利用等差數列的通項公式可得Sn ， 再利用遞推關系可得bn ． （2） = = ．利用“裂項求和”方法即可得出．
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識，掌握數列{an}的前n項和sn與通項an的關系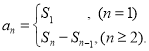，以及對數列的通項公式的理解，了解如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式．