
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是圓內(nèi)接四邊形,
是圓內(nèi)接四邊形,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)設(shè)線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的中點為
的中點為![]() ,且
,且![]() 在線段
在線段![]() 上運動,求直線
上運動,求直線![]() 與平面
與平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,通過證明
,通過證明![]() 、
、![]() 證得
證得![]() 平面
平面![]() ,由此證得
,由此證得![]() .證得
.證得![]() ,從而證得
,從而證得![]() 平面
平面![]() ,進(jìn)而證得平面
,進(jìn)而證得平面![]() 平面
平面![]() .
.
(2)建立空間直角坐標(biāo)系,設(shè)![]() ,通過直線
,通過直線![]() 的方向向量和平面
的方向向量和平面![]() 平面而的法向量求得直線
平面而的法向量求得直線![]() 與平面
與平面![]() 所成角的正弦值
所成角的正弦值
(1)證明:如圖,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,
,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
易得![]() ,∴
,∴![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() .
.
又底面![]() 是圓內(nèi)接四邊形,∴
是圓內(nèi)接四邊形,∴![]() ,
,
在![]() 中,由
中,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,易得
,易得![]() ,∴
,∴![]() ,
,
即![]() .又
.又![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
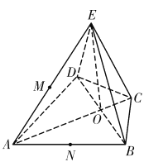
(2)解:點![]() 在線段
在線段![]() 上.以
上.以![]() 為坐標(biāo)原點,
為坐標(biāo)原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸,建立空間直角坐標(biāo)系,則
軸,建立空間直角坐標(biāo)系,則![]() ,
,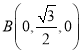 ,
,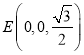 ,
,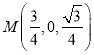 ,
,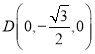 ,
,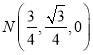 ,∴
,∴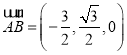 ,
,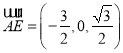 ,
,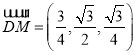 ,
,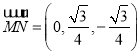 ,設(shè)平面
,設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則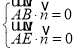 ,即
,即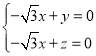 ,令
,令![]() ,則
,則![]() ,
,
設(shè)![]() ,可得
,可得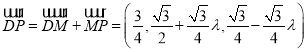 ,
,
設(shè)直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,則
,則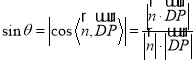
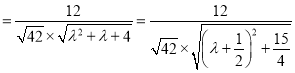 ,
,
∵![]() ,∴當(dāng)
,∴當(dāng)![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.
故直線![]() 與平面
與平面![]() 所成角的正弦值的最大值為
所成角的正弦值的最大值為![]() .
.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解學(xué)生自主學(xué)習(xí)期間完成數(shù)學(xué)套卷的情況,一名教師對某班級的所有學(xué)生進(jìn)行了調(diào)查,調(diào)查結(jié)果如下表.
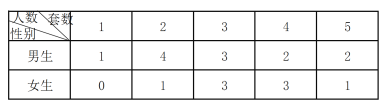
(1)從這班學(xué)生中任選一名男生,一名女生,求這兩名學(xué)生完成套卷數(shù)之和為4的概率?
(2)若從完成套卷數(shù)不少于4套的學(xué)生中任選4人,設(shè)選到的男學(xué)生人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(3)試判斷男學(xué)生完成套卷數(shù)的方差![]() 與女學(xué)生完成套卷數(shù)的方差
與女學(xué)生完成套卷數(shù)的方差![]() 的大小(只需寫出結(jié)論).
的大小(只需寫出結(jié)論).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,已知定點
中,已知定點![]() 、
、![]() ,動點
,動點![]() 滿足
滿足![]() ,設(shè)點
,設(shè)點![]() 的曲線為
的曲線為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 兩點.
兩點.![]()
(1)寫出曲線![]() 的方程,并指出曲線
的方程,并指出曲線![]() 的軌跡;
的軌跡;
(2)當(dāng)![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)證明:存在直線![]() ,滿足
,滿足![]() ,并求實數(shù)
,并求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xoy中,以坐標(biāo)原點O為極點,x軸正半軸為極軸建立極坐標(biāo)系。已知曲線C的極坐標(biāo)方程為![]() ,過點
,過點![]() 的直線l的參數(shù)方程為
的直線l的參數(shù)方程為 (為參數(shù)),直線l與曲線C交于M、N兩點。
(為參數(shù)),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標(biāo)方程:
(2)若![]() 成等比數(shù)列,求a的值。
成等比數(shù)列,求a的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,點
中,點![]() 到點
到點![]() 的距離比它到
的距離比它到![]() 軸的距離多1,記點
軸的距離多1,記點![]() 的軌跡為
的軌跡為![]() ;
;
(1)求軌跡![]() 的方程;
的方程;
(2)求定點![]() 到軌跡
到軌跡![]() 上任意一點
上任意一點![]() 的距離
的距離![]() 的最小值;
的最小值;
(3)設(shè)斜率為![]() 的直線
的直線![]() 過定點
過定點![]() ,求直線
,求直線![]() 與軌跡
與軌跡![]() 恰好有一個公共點,兩個公共點,三個公共點時
恰好有一個公共點,兩個公共點,三個公共點時![]() 的相應(yīng)取值范圍.
的相應(yīng)取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若一個四位數(shù)的各位數(shù)字相加和為10,則稱該數(shù)為“完美四位數(shù)”,如數(shù)字“2017”.試問用數(shù)字0,1,2,3,4,5,6,7組成的無重復(fù)數(shù)字且大于2017的“完美四位數(shù)”有( )個.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某農(nóng)戶考察三種不同的果樹苗A、B、C,經(jīng)引種試驗后發(fā)現(xiàn),引種樹苗A的自然成活率為0.8,引種樹苗B、C的自然成活率均為0.9.
(1)若引種樹苗A、B、C各10棵.
①估計自然成活的總棵數(shù);
②利用①的估計結(jié)論,從沒有自然成活的樹苗中隨機抽取兩棵,求抽到的兩棵都是樹苗A的概率;
(2)該農(nóng)戶決定引種B種樹苗,引種后沒有自然成活的樹苗中有75%的樹苗可經(jīng)過人工栽培技術(shù)處理,處理后成活的概率為0.8,其余的樹苗不能成活.若每棵樹苗引種最終成活后可獲利300元,不成活的每棵虧損50元,該農(nóng)戶為了獲利不低于20萬元,問至少引種B種樹苗多少棵?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】算籌是在珠算發(fā)明以前我國獨創(chuàng)并且有效的計算工具,為我國古代數(shù)學(xué)的發(fā)展做出了很大貢獻(xiàn).在算籌計數(shù)法中,以“縱式”和“橫式”兩種方式來表示數(shù)字,如圖:

表示多位數(shù)時,個位用縱式,十位用橫式,百位用縱式,千位用橫式,以此類推,遇零則置空,如圖:
![]()
如果把5根算籌以適當(dāng)?shù)姆绞饺糠湃?下面的表格中,那么可以表示的三位數(shù)的個數(shù)為( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com