在正項數(shù)列{a
n}中,若a
1=1,且對所有n∈N
*滿足na
n+1-(n+1)a
n=0,則a
2014=( )
| A.1011 | B.1012 | C.2013 | D.2014 |
由a
1=1,na
n+1-(n+1)a
n=0可得
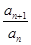
=

,得到
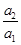
=
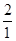
,
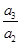
=
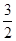
,
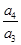
=
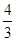
,…,
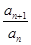
=

,上述式子兩邊分別相乘得
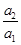
×
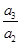
×
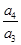
×…×
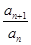
=a
n+1=
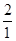
×
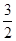
×
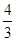
×…×

=n+1,故a
n=n,所以a
2014=2014,故選D.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
通項公式為
an=的數(shù)列{a
n}的前n項和為
,則項數(shù)n為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知點(1,
)是函數(shù)f(x)=a
x(a>0且a≠1)的圖象上一點,等比數(shù)列{a
n}的前n項和為f(n)-c,數(shù)列{b
n}(b
n>0)的首項為c,且前n項和S
n滿足S
n-S
n-1=
+
(n≥2)
(Ⅰ)求數(shù)列{a
n}和{b
n}的通項公式
(Ⅱ)求數(shù)列{
}前n項和為T
n.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設項數(shù)均為k(k≥2,k∈N*)的數(shù)列{an}、{bn}、{cn}前n項的和分別為Sn、Tn、Un.已知:an-bn=2n(1≤n≤k,n∈N*),且集合{a1,a2,…,ak,b1,b2,…,bk}={2,4,6,…,4k-2,4k}.
(1)已知Un=2n+2n,求數(shù)列{cn}的通項公式;
(2)若k=4,求S4和T4的值,并寫出兩對符合題意的數(shù)列{an}、{bn};
(3)對于固定的k,求證:符合條件的數(shù)列對({an},{bn})有偶數(shù)對.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若單調遞增數(shù)列

滿足

,且

,則

的取值范圍是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知數(shù)列

的前

項和為

,且

則

等于( )
| A.4 | B.2 | C.1 | D. |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知數(shù)列
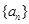
的前n項和為
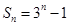
,那么該數(shù)列的通項公式為
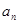
=_______.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設數(shù)列
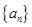
為等差數(shù)列,且

,

,數(shù)列

的前

項和為

,

且

.
(1)求數(shù)列
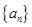
,

的通項公式;
(2)若

,

為數(shù)列

的前

項和,

對

恒成立,求

的最小值.
查看答案和解析>>

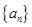 為等差數(shù)列,且
為等差數(shù)列,且 ,
, ,數(shù)列
,數(shù)列 的前
的前 項和為
項和為 ,
, 且
且 .
.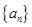 ,
, 的通項公式;
的通項公式; ,
, 為數(shù)列
為數(shù)列 的前
的前 項和,
項和, 對
對 恒成立,求
恒成立,求 的最小值.
的最小值.