
要制作一個如圖的框架(單位:m),要求所圍成的總面積為19.5(m2),其中ABCD是一個矩形,EFCD是一個等腰梯形,梯形高h=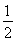 AB,tan∠FED=
AB,tan∠FED=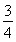 ,設AB=xm,BC=ym.
,設AB=xm,BC=ym.

(1)求y關于x的表達式;
(2)如何設計x、y的長度,才能使所用材料最少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第3課時練習卷(解析版) 題型:填空題
若函數f(x)=ax(a>0,a≠1)在[-1,2]上的最大值為4,最小值為m,且函數g(x)=(1-4m)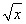 在[0,+∞)上是增函數,則a=________.
在[0,+∞)上是增函數,則a=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第1課時練習卷(解析版) 題型:解答題
判斷下列對應是否是從集合A到集合B的函數.
(1) A=B=N*,對應法則f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,對應法則f:x→y,這里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],對應法則f:x→y,這里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,對應法則:對任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第14課時練習卷(解析版) 題型:填空題
關于函數f(x)=lg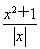 (x>0,x∈R),下列命題正確的是________.(填序號)
(x>0,x∈R),下列命題正確的是________.(填序號)
①函數y=f(x)的圖象關于y軸對稱;
②在區間(-∞,0)上,函數y=f(x)是減函數;
③函數y=f(x)的最小值為lg2;
④在區間(1,+∞)上,函數y=f(x)是增函數.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第13課時練習卷(解析版) 題型:解答題
某建筑公司要在一塊寬大的矩形地面(如圖所示)上進行開發建設,陰影部分為一公共設施建設不能開發,且要求用欄柵隔開(欄柵要求在一直線上),公共設施邊界為曲線f(x)=1-ax2(a>0)的一部分,欄柵與矩形區域的邊界交于點M、N,交曲線于點P,設P(t,f(t)).
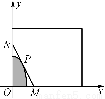
(1)將△OMN(O為坐標原點)的面積S表示成t的函數S(t);
(2)若在t=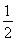 處,S(t)取得最小值,求此時a的值及S(t)的最小值.
處,S(t)取得最小值,求此時a的值及S(t)的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第13課時練習卷(解析版) 題型:解答題
如圖,ABCD是正方形空地,邊長為30m,電源在點P處,點P到邊AD、AB距離分別為9m、3m.某廣告公司計劃在此空地上豎一塊長方形液晶廣告屏幕MNEF,MN∶NE=16∶9.線段MN必須過點P,端點M、N分別在邊AD、AB上,設AN=x(m),液晶廣告屏幕MNEF的面積為S(m2).
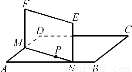
(1)用x的代數式表示AM;
(2)求S關于x的函數關系式及該函數的定義域;
(3)當x取何值時,液晶廣告屏幕MNEF的面積S最小?
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第13課時練習卷(解析版) 題型:填空題
某商品在近30天內每件的銷售價格P(元)與時間t(天)的函數關系為P=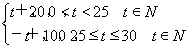 且該商品的日銷售量Q與時間t(天)的函數關系為Q=-t+40(0<t≤30,t∈N),則這種商品日銷量金額最大的一天是30天中的第________天.
且該商品的日銷售量Q與時間t(天)的函數關系為Q=-t+40(0<t≤30,t∈N),則這種商品日銷量金額最大的一天是30天中的第________天.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第12課時練習卷(解析版) 題型:解答題
若函數f(x)=-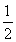
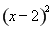 +blnx在(1,+∞)上是減函數,求實數b的取值范圍.
+blnx在(1,+∞)上是減函數,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第二章第10課時練習卷(解析版) 題型:填空題
若函數f(x)=x3+x2-2x-2的一個正數零點附近的函數值用二分法計算,其參考數據如下:
f(1)=-2 | f(1.5)=0.625 | f(1.25)=-0.984 |
f(1.375)=-0.260 | f(1.4375)=0.162 | f(1.40625)=-0.054 |
那么方程x3+x2-2x-2=0的一個近似根為________(精確到0.1).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com