分析:①中根據,{bn}是等差數列可推斷出an-an-1也是常數,進而推斷出數列{an}為等差數列;②中根據數列的遞推可求得an+1-an-1為常數但不是相鄰的兩項,故數列{an}不一定是等差數列②不正確;③根據數列的遞推式可求得數列{an}的通項公式,推斷出不是等差數列;④中根據2an-1=n2-(n-1)2求得數列的通項公式,進而推斷出數列為等差數列.最后綜合可得答案.
解答:解:對于①{b
n}是等差數列,∴b
n-b
n-1=2a
n-2a
n-1=d(常數)
∴a
n-a
n-1=
,故數列{a
n}為等差數列,①正確.
∵b
n-1=a
n-1+a
n,∴b
n=a
n+a
n+1,兩式相減得a
n+1-a
n-1=d,數列{a
n}不一定是等差數列②不正確
③中S
n=n
2+1,∴當n≥2時,a
n=S
n-S
n-1=2n-1,但a
1=1
2+1=2不符合a
n=2n-1
∴a
n=
∴數列{a
n}不是等差數列
④2a
n-1=n
2-(n-1)
2=2n-1,n≥2,a
n=n,當n=1時a
1=1符合
∴a
n=n,∴數列{a
n}為等差數列
故答案為:①④
點評:本題主要考查了等差數列的定義和等差數列的通項公式的應用.考查了學生對等差數列的基礎知識的綜合運用.



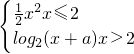 在定義域內是連續函數,數列{an}通項公式為an=
在定義域內是連續函數,數列{an}通項公式為an=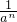 ,則數列{an}的所有項之和為1.
,則數列{an}的所有項之和為1.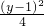 =1有唯一公共點的直線有且只有兩條.
=1有唯一公共點的直線有且只有兩條.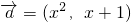 ,
,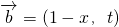 ,若函數f(x)=
,若函數f(x)= 在區間[-1,1]上是增函數,則實數t的取值范圍是(5,+∞);
在區間[-1,1]上是增函數,則實數t的取值范圍是(5,+∞); 在定義域內是連續函數,數列{an}通項公式為an=
在定義域內是連續函數,數列{an}通項公式為an= ,則數列{an}的所有項之和為1.
,則數列{an}的所有項之和為1.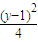 =1有唯一公共點的直線有且只有兩條.
=1有唯一公共點的直線有且只有兩條. ,
, ,若函數f(x)=
,若函數f(x)= 在區間[-1,1]上是增函數,則實數t的取值范圍是(5,+∞);
在區間[-1,1]上是增函數,則實數t的取值范圍是(5,+∞); +
+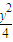 =1,直線l的方程是y=x+3.
=1,直線l的方程是y=x+3.