【題目】如圖，已知橢圓
上頂點為A，右焦點為F，直線
與圓
相切，其中
.
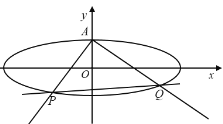
（1）求橢圓的方程；
（2）不過點A的動直線l與橢圓C相交于P，Q兩點，且
，證明：動直線l過定點，并且求出該定點坐標.
【答案】（1）
；（2）
【解析】
（1）確定圓M的圓心與半徑，利用直線AF與圓M相切關系，根據點到直線的距離公式構建方程，求得a，即可表示方程；
（2）設直線AP的方程為
，則直線AQ的方程為
，分別于橢圓聯立方程求得交點P、Q的坐標，即可表示直線l的方程，得答案.
（1）由題可知，
，則直線
的方程為
，即
因為直線與圓
相切，該圓的圓心為
則
故橢圓的標準方程為
（2）因為不過點A的動直線l與橢圓C相交于P，Q兩點，且
，即直線AP與坐標軸不垂直也不平行
由
可設直線AP的方程為，則直線AQ的方程為
聯立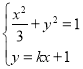
，消去y并整理得
，解得
或
，
因此點P的坐標為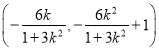
，即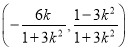
將上式中的k換成
，得點Q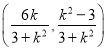
所以直線l的斜率為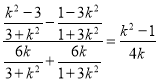
，
即直線l的方程為
，
化簡并整理得
，
故直線l恒過定點
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】若函數
在
時，函數值y的取值區間恰為[
]，就稱區間
為的一個“倒域區間”．定義在
上的奇函數
，當
時，
．
（Ⅰ）求的解析式；
（Ⅱ）求函數在
內的“倒域區間”；
（Ⅲ）若函數在定義域內所有“倒域區間”上的圖像作為函數
=
的圖像，是否存在實數
，使集合
恰含有2個元素．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個袋子里裝有7個球，其中有紅球4個.白球3個.這些球除顏色外全相同.
（1）若一次從袋中取出3個球，取出的球顏色不完全相同的概率；
（2）若一次從袋中取出3個球.其中若取到紅球得0分，取到白球得1分，記隨機變量
為取出的三個小球得分之和，求的分布列，并求其數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設a，b∈（0，1）∪（1，+∞），定義運算：
，則以下四個結論：①（2τ4）τ8=8τ（4τ2）；②8τ（4τ2）＞（8τ4）τ2＞（2τ8）τ4；③（4τ2）=（2τ4）τ4＜（2τ8）τ4；④
．其中所有正確結論的序號為__．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的圖象的一個對稱中心與它相鄰的一條對稱軸之間的距離為
．
（1）求函數f（x）的對稱軸方程及單調遞增區間；
（2）將函數y=f（x）的圖象向右平移
個單位后，再將得到的圖象上所有點的橫坐標縮短到原來的
（縱坐標不變），得到函數y=g（x）的圖象，當x∈（
，
）時，求函數g（x）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某服裝廠生產一種服裝，每件服裝的成本為80元，出廠單價為120元.該廠為鼓勵銷售商訂購，決定當一次訂購超過100件時，每多訂購一件，訂購的全部服裝的出廠單價就降低0.04元.根據市場調查，銷售商一次訂購量不會超過600件．
（1）設一次訂購為
件服裝的實際出廠單價為
元，寫出函數
的表達式；
（2）當銷售商一次訂購多少件服裝時，該服裝廠獲得的利潤最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了了解某市民眾對某項公共政策的態度，在該市隨機抽取了50名市民進行調查，作出他們的月收入（單位：百元，范圍：
）的頻率分布直方圖，同時得到他們月收入情況以及對該項政策贊成的人數統計表：
月收入 | 贊成的人數 |
| 4 |
| 8 |
| 12 |
| 5 |
| 2 |
| 2 |
（1）求月收入在
內的頻率，補全頻率分布直方圖，并在圖中標出相應縱坐標；
（2）若從月收入在
內的被調查者中隨機選取2人，求這2人對該項政策都不贊成的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
