
【題目】某服裝廠生產一種服裝,每件服裝的成本為80元,出廠單價為120元.該廠為鼓勵銷售商訂購,決定當一次訂購超過100件時,每多訂購一件,訂購的全部服裝的出廠單價就降低0.04元.根據市場調查,銷售商一次訂購量不會超過600件.
(1)設一次訂購為![]() 件服裝的實際出廠單價為
件服裝的實際出廠單價為![]() 元,寫出函數
元,寫出函數![]() 的表達式;
的表達式;
(2)當銷售商一次訂購多少件服裝時,該服裝廠獲得的利潤最大?
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() ,
, ![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切;
相切;
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在曲線![]() 上取兩點
上取兩點![]() ,
, ![]() 與原點
與原點![]() 構成
構成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)利用極坐標與直角坐標的互化公式可得直線![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
,消去參數![]() 可知曲線
可知曲線![]() 是圓心為
是圓心為![]() ,半徑為
,半徑為![]() 的圓,由直線
的圓,由直線![]() 與曲線
與曲線![]() 相切,可得:
相切,可得: ![]() ;則曲線C的方程為
;則曲線C的方程為![]() , 再次利用極坐標與直角坐標的互化公式可得
, 再次利用極坐標與直角坐標的互化公式可得
可得曲線C的極坐標方程.
(2)由(1)不妨設M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面積的最大值.
面積的最大值.
試題解析:(1)由題意可知直線![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
曲線![]() 是圓心為
是圓心為![]() ,半徑為
,半徑為![]() 的圓,直線
的圓,直線![]() 與曲線
與曲線![]() 相切,可得:
相切,可得:  ;可知曲線C的方程為
;可知曲線C的方程為![]() ,
,
所以曲線C的極坐標方程為![]() ,
,
即![]() .
.
(2)由(1)不妨設M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
當![]() 時,
時, ![]() ,
,
所以△MON面積的最大值為![]() .
.
【題型】解答題
【結束】
23
【題目】已知函數![]() 的定義域為
的定義域為![]() ;
;
(1)求實數![]() 的取值范圍;
的取值范圍;
(2)設實數![]() 為
為![]() 的最大值,若實數
的最大值,若實數![]() ,
, ![]() ,
, ![]() 滿足
滿足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 上頂點為A,右焦點為F,直線
上頂點為A,右焦點為F,直線![]() 與圓
與圓![]() 相切,其中
相切,其中![]() .
.
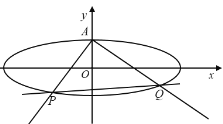
(1)求橢圓的方程;
(2)不過點A的動直線l與橢圓C相交于P,Q兩點,且![]() ,證明:動直線l過定點,并且求出該定點坐標.
,證明:動直線l過定點,并且求出該定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠加工一批零件,加工過程中會產生次品,根據經驗可知,其次品率![]() 與日產量
與日產量![]() (萬件)之間滿足函數關系式
(萬件)之間滿足函數關系式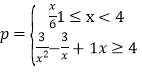 ,已知每生產1萬件合格品可獲利2萬元,但生產1萬件次品將虧損1萬元.(次品率=次品數/生產量).
,已知每生產1萬件合格品可獲利2萬元,但生產1萬件次品將虧損1萬元.(次品率=次品數/生產量).
(1)試寫出加工這批零件的日盈利額![]() (萬元)與日產量
(萬元)與日產量![]() (萬件)的函數;
(萬件)的函數;
(2)當日產量為多少時,可獲得最大利潤?最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() (c為常數),且f(1)=0.
(c為常數),且f(1)=0.
(1)求c的值;
(2)證明函數f(x)在[0,2]上是單調遞增函數;
(3)已知函數g(x)=f(ex),判斷函數g(x)的奇偶性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市的華為手機專賣店對該市市民使用華為手機的情況進行調查.在使用華為手機的用戶中,隨機抽取100名,按年齡(單位:歲)進行統計的頻率分布直方圖如圖:

(1)根據頻率分布直方圖,分別求出樣本的平均數(同一組數據用該區間的中點值作代表)和中位數的估計值(均精確到個位);
(2)在抽取的這100名市民中,按年齡進行分層抽樣,抽取20人參加華為手機宣傳活動,再從這20人中年齡在![]() 和
和![]() 的人群里,隨機選取2人各贈送一部華為手機,求這2名市民年齡都在
的人群里,隨機選取2人各贈送一部華為手機,求這2名市民年齡都在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)判斷![]() 的奇偶性并說明理由;
的奇偶性并說明理由;
(2)若![]() ,試判斷函數
,試判斷函數![]() 的單調性,并用定義法證明;
的單調性,并用定義法證明;
(3)若已知![]() ,且函數
,且函數![]() 在區間[1,+∞)上的最小值為-2,求實數m的值.
在區間[1,+∞)上的最小值為-2,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com