
【題目】某公司計劃在今年內同時出售變頻空調機和智能洗衣機,由于這兩種產品的市場需求量非常大,有多少就能銷售多少,因此該公司要根據實際情況(如資金、勞動力)確定產品的月供應量,以使得總利潤達到最大.已知對這兩種產品有直接限制的因素是資金和勞動力,通過調查,得到關于這兩種產品的有關數據如表:
試問:怎樣確定兩種貨物的月供應量,才能使總利潤達到最大,最大利潤是多少?
資金 | 單位產品所需資金(百元) | ||
空調機 | 洗衣機 | 月資金供應量(百元) | |
成本 | 30 | 20 | 300 |
勞動力(工資) | 5 | 10 | 110 |
單位利潤 | 6 | 8 | |
 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:高中數學 來源: 題型:
【題目】設an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正數的個數是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正數的個數是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三文科分為五個班.高三數學測試后,隨機地在各班抽取部分學生進行成績統計,各班被抽取的學生人數恰好成等差數列,人數最少的班被抽取了18人.抽取出來的所有學生的測試成績統計結果的頻率分布條形圖如圖所示,其中120~130(包括120分但不包括130分)的頻率為0.05,此分數段的人數為5人.
(1)問各班被抽取的學生人數各為多少人?
(2)在抽取的所有學生中,任取一名學生,求分數不小于90分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 【2017四川宜賓二診】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,已知點
中,已知點![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為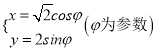 .以原點為極點,
.以原點為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為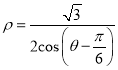 .
.
(Ⅰ)判斷點![]() 與直線
與直線![]() 的位置關系并說明理由;
的位置關系并說明理由;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 的兩個交點分別為
的兩個交點分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正數數列{an}的前n項和為Sn , 點P(an , Sn)在函數f(x)= ![]() x2+
x2+ ![]() x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
x上,已知b1=1,3bn﹣2bn﹣1=0(n≥2,n∈N*),
(1)求數列{an}的通項公式;
(2)若cn=anbn , 求數列{cn}的前n項和Tn;
(3)是否存在整數m,M,使得m<Tn<M對任意正整數n恒成立,且M﹣m=9,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0),四點P1(1,1),P2(0,1),P3(–1,
(a>b>0),四點P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.
)中恰有三點在橢圓C上.
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為–1,證明:l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側棱垂直底面,∠ACB=90°,AC=BC= ![]() AA1 , D是棱AA1的中點.
AA1 , D是棱AA1的中點.
(Ⅰ)證明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱為兩部分,求這兩部分體積的比.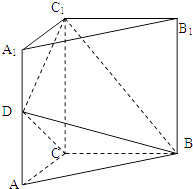
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD的底面是正方形,每條側棱的長都是底面邊長的 ![]() 倍,P為側棱SD上的點.
倍,P為側棱SD上的點. 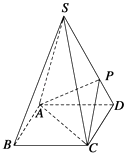
(1)求證:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P﹣AC﹣D的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com