
【題目】已知△OAB的頂點坐標為O(0,0),A(2,9),B(6,﹣3),點P的橫坐標為14,且 ![]() ,點Q是邊AB上一點,且
,點Q是邊AB上一點,且 ![]() .
.
(1)求實數λ的值與點P的坐標;
(2)求點Q的坐標;
(3)若R為線段OQ上的一個動點,試求 ![]() 的取值范圍.
的取值范圍.
【答案】
(1)解:設P(14,y),則 ![]() ,由
,由 ![]() ,得(14,y)=λ(﹣8,﹣3﹣y),解得
,得(14,y)=λ(﹣8,﹣3﹣y),解得 ![]() ,所以點P(14,﹣7)
,所以點P(14,﹣7)
(2)解:設點Q(a,b),則 ![]() ,又
,又 ![]() ,則由
,則由 ![]() ,得3a=4b①又點Q在邊AB上,所以
,得3a=4b①又點Q在邊AB上,所以 ![]() ,即3a+b﹣15=0②
,即3a+b﹣15=0②
聯立①②,解得a=4,b=3,所以點Q(4,3).
(3)解:因為R為線段OQ上的一個動點,故設R(4t,3t),且0≤t≤1,則, ![]() ,
, ![]() ,
, ![]() ,則
,則 ![]() =
= ![]() ,故
,故 ![]() 的取值范圍為
的取值范圍為 ![]()
【解析】(1)先設P(14,y),分別表示 ![]() ,
, ![]() 然后由
然后由 ![]() ,建立關于y的方程可求y.(2)先設點Q(a,b),則可表示向量
,建立關于y的方程可求y.(2)先設點Q(a,b),則可表示向量 ![]() ,由
,由 ![]() ,可得3a=4b,再由點Q在邊AB上可得
,可得3a=4b,再由點Q在邊AB上可得 ![]() ①②,從而可解a,b,進而可得Q的坐標.(3)由R為線段OQ上的一個動點可設R(4t,3t),且0≤t≤1,則有分別表示
①②,從而可解a,b,進而可得Q的坐標.(3)由R為線段OQ上的一個動點可設R(4t,3t),且0≤t≤1,則有分別表示 ![]() ,
, ![]() ,由向量的數量積整理可得
,由向量的數量積整理可得 ![]() ,利用二次函數的知識可求取值范圍.
,利用二次函數的知識可求取值范圍.


 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列對應值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根據表格提供的數據求函數f(x)的一個解析式.
(2)根據(1)的結果,若函數y=f(kx)(k>0)周期為 ![]() ,當
,當 ![]() 時,方程f(kx)=m恰有兩個不同的解,求實數m的取值范圍.
時,方程f(kx)=m恰有兩個不同的解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A.若 ![]() 與
與 ![]() 互為負向量,則
互為負向量,則 ![]() +
+ ![]() =0
=0
B.若 ![]()
![]() =0,則
=0,則 ![]() =
= ![]() 或
或 ![]() =
= ![]()
C.若 ![]() ,
, ![]() 都是單位向量,則
都是單位向量,則 ![]()
![]() =1
=1
D.若k為實數且k ![]() =
= ![]() ,則k=0或
,則k=0或 ![]() =
= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】養正中學新校區內有一塊以O為圓心,R(單位:米)為半徑的半圓形荒地(如圖),校總務處計劃對其開發利用,其中弓形BCD區域(陰影部分)用于種植觀賞植物,△OBD區域用于種植花卉出售,其余區域用于種植草皮出售。已知種植觀賞植物的成本是每平方米20元,種植花卉的利潤是每平方米80元,種植草皮的利潤是每平方米30元。
(1)設![]() (單位:弧度),用
(單位:弧度),用![]() 表示弓形BCD的面積
表示弓形BCD的面積![]()
(2)如果該校總務處邀請你規劃這塊土地。如何設計![]() 的大小才能使總利潤最大?并求出該最大值
的大小才能使總利潤最大?并求出該最大值

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體AC1中,過點A作平面A1BD的垂線,垂足為點H,則以下命題中,錯誤的命題是( ) 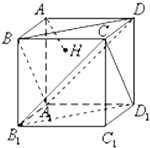
A.點H是△A1BD的垂心
B.AH的延長線經過點C1
C.AH垂直平面CB1D1
D.直線AH和BB1所成角為45°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|,g(x)=ax,(a∈R).
(1)若函數y=f(x)是偶函數,求出符合條件的實數a的值;
(2)若方程f(x)=g(x)有兩解,求出實數a的取值范圍;
(3)若a>0,記F(x)=g(x)f(x),試求函數y=F(x)在區間[1,2]上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省的一個氣象站觀測點在連續4天里記錄的![]() 指數
指數![]() 與當天的空氣水平可見度
與當天的空氣水平可見度![]() (單位:
(單位: ![]() )的情況如表1:
)的情況如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
該省某市2017年9月![]() 指數頻數分布如表2:
指數頻數分布如表2:
|
|
|
|
|
|
頻數 | 3 | 6 | 12 | 6 | 3 |
(1)設![]() ,根據表1的數據,求出
,根據表1的數據,求出![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)小李在該市開了一家洗車店,經統計,洗車店平均每天的收入與![]() 指數有相關關系,如表3:
指數有相關關系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根據表3估計小李的洗車店9月份平均每天的收入.
(附參考公式: ![]() ,其中
,其中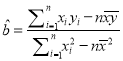 ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+ ![]() (其中a,b為常數)的圖象經過(1,2),(2,
(其中a,b為常數)的圖象經過(1,2),(2, ![]() )兩點.
)兩點.
(1)求函數f(x)的解析式;
(2)判斷f(x)的奇偶性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com