
【題目】已知函數![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)討論![]() 的單調性;
的單調性;
(3)設過![]() 兩點的直線的斜率為
兩點的直線的斜率為![]() ,其中
,其中![]() 、
、![]() 為曲線
為曲線![]() 上的任意兩點,并且
上的任意兩點,并且![]() ,若
,若![]() 恒成立,證明:
恒成立,證明: ![]() .
.
【答案】(1)![]() (2)見解析(3)見解析
(2)見解析(3)見解析
【解析】試題分析:(1)由導數幾何意義得切線斜率為![]() ,再根據點斜式求切線方程(2)因為導函數為
,再根據點斜式求切線方程(2)因為導函數為![]() ,所以根據
,所以根據![]() ,
, ![]() 討論:
討論: ![]() ,在
,在![]() 上遞增;
上遞增; ![]() 遞增;
遞增; ![]() 遞減.(3)由(2)知
遞減.(3)由(2)知![]() 的單調性,又
的單調性,又![]() ,所以由
,所以由![]() 恒成立得
恒成立得![]() ,利用斜率公式化簡
,利用斜率公式化簡![]() 得
得![]() ,轉化為利用導數證明
,轉化為利用導數證明![]() ,易證.
,易證.
試題解析:解:(1)當![]() 時,
時, ![]() ,
,
對函數![]() 求導得
求導得![]() ,
,
![]() ,又
,又![]() ,
,
![]() 曲線
曲線![]() 在
在![]() 處的切線方程為:
處的切線方程為: ![]() ;
;
(2)求導得![]() .
.
若![]() ,
, ![]() ,
, ![]() 在
在![]() 上遞增;
上遞增;
若![]() ,當
,當![]() 時,
時, ![]() ,
, ![]() 單調遞增;
單調遞增;
當![]() 時,
時, ![]() ,
, ![]() 單調遞減.
單調遞減.
(3)由(2)知,若![]() ,
, ![]() 在
在![]() 上遞增,
上遞增,
又![]() ,故
,故![]() 不恒成立.
不恒成立.
若![]() ,當
,當![]() 時,
時, ![]() 遞減,
遞減, ![]() ,不合題意.
,不合題意.
若![]() ,當
,當![]() 時,
時, ![]() 遞增,
遞增, ![]() ,不合題意.
,不合題意.
若![]() ,
, ![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
![]() ,合題意.
,合題意.
故![]() ,且
,且![]() (當且僅當
(當且僅當![]() 時取“=”).
時取“=”).
設![]() ,
, 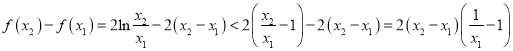
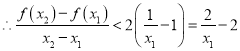 ,
,
因此, ![]() .
.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知點A,B,C在圓x2+y2=1上運動,且AB⊥BC,若點P的坐標為 ![]() ,則
,則 ![]() 的取值范圍為( )
的取值范圍為( )
A.[8,10]
B.[9,11]
C.[8,11]
D.[9,12]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解春季晝夜溫差大小與種子發芽多少之間的關系,現從4月的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天每50顆種子浸泡后的發芽數,得到如下表格:
日期 | 4月1日 | 4月6日 | 4月12日 | 4月19日 | 4月27日 |
溫差 | 2 | 3 | 5 | 4 | 1 |
發芽數 | 9 | 11 | 15 | 13 | 7 |
(1)從這5天中任選2天,記發芽的種子數分別為![]() ,求事件“
,求事件“![]() 均小于13”的概率;
均小于13”的概率;
(2)若4月30日晝夜溫差為![]() ,請根據
,請根據![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() 估計該天種子浸泡后的發芽數.
估計該天種子浸泡后的發芽數.
參考公式:  ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com