
(本題滿分12分)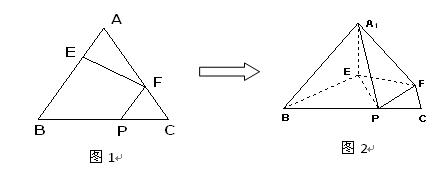
在正三角形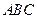 中,
中,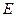 、
、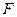 、
、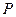 分別是
分別是 、
、 、
、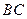 邊上的點,滿足AE:EB=CF:FA=CP:PB=1:2(如圖1)。將△
邊上的點,滿足AE:EB=CF:FA=CP:PB=1:2(如圖1)。將△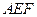 沿
沿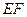 折起到
折起到 的位置,使二面角A1-EF-B成直二面角,連結A1B、A1P(如圖2)
的位置,使二面角A1-EF-B成直二面角,連結A1B、A1P(如圖2)
(Ⅰ)求證:A1E⊥平面BEP;
(Ⅱ)求直線A1E與平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函數表示)
.解法一:不妨設正三角形ABC的邊長為3
(1) 在圖1中,取BE中點D,連結DF. AE:EB=CF:FA=1:2∴AF=AD=2而∠A=600 , ∴△ADF是正三角形,又AE="DE=1," ∴EF⊥AD在圖2中,A1E⊥EF, BE⊥EF, ∴∠A1EB為二面角A1-EF-B的平面角。由題設條件知此二面角為直二面角,A1E⊥BE,又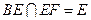 ∴A1E⊥平面BEF,即 A1E⊥平面BEP
∴A1E⊥平面BEF,即 A1E⊥平面BEP
(2) 在圖2中,A1E不垂直A1B, ∴A1E是平面A1BP的垂線,又A1E⊥平面BEP,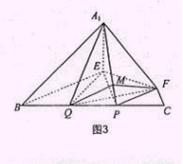 ∴A1E⊥BE.從而BP垂直于A1E在平面A1BP內的射影(三垂線定理的逆定理)設A1E在平面A1BP內的射影為A1Q,且A1Q交BP于點Q,則∠E1AQ就是A1E與平面A1BP所成的角,且BP⊥A1Q.在△EBP中, BE=EP=2而∠EBP=600 , ∴△EBP是等邊三角形.又 A1E⊥平面BEP , ∴A1B=A1P, ∴Q為BP的中點,且
∴A1E⊥BE.從而BP垂直于A1E在平面A1BP內的射影(三垂線定理的逆定理)設A1E在平面A1BP內的射影為A1Q,且A1Q交BP于點Q,則∠E1AQ就是A1E與平面A1BP所成的角,且BP⊥A1Q.在△EBP中, BE=EP=2而∠EBP=600 , ∴△EBP是等邊三角形.又 A1E⊥平面BEP , ∴A1B=A1P, ∴Q為BP的中點,且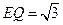 ,又 A1E=1,在Rt△A1EQ中,
,又 A1E=1,在Rt△A1EQ中,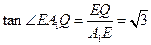 ,∴∠EA1Q=60o,
,∴∠EA1Q=60o,
∴直線A1E與平面A1BP所成的角為600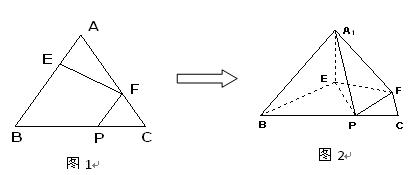
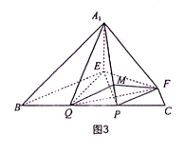
(3)在圖3中,過F作FM⊥ A1P與M,連結QM,QF,∵CP=CF=1,
∠C=600,∴△FCP是正三角形,∴PF=1.有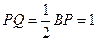
∴PF=PQ①,
∵A1E⊥平面BEP, 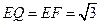 ∴A1E=A1Q,
∴A1E=A1Q,
∴△A1FP≌△A1QP從而∠A1PF=∠A1PQ②,
由①②及MP為公共邊知△FMP≌△QMP,
∴∠QMP=∠FMP=90o,且MF=MQ,
從而∠FMQ為二面角B-A1P-F的平面角.
在Rt△A1QP中,A1Q=A1F=2,PQ=1,又∴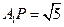 . ∵ MQ⊥A1P∴
. ∵ MQ⊥A1P∴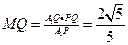 ∴
∴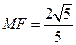 在△FCQ中,FC="1,QC=2," ∠C=600,由余弦定理得
在△FCQ中,FC="1,QC=2," ∠C=600,由余弦定理得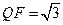
在△FMQ中,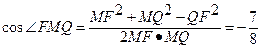
∴二面角B-A1P-F的大小為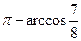
解析


 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源: 題型:
(本題滿分12分)
在△ABC中,角A、B、C的對邊分別為a、b、c,且![]() .
.
??????(Ⅰ)求角A的大小;??????(Ⅱ)若![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分)
在平面直角坐標系中,已知A1(-3,0),A2(3,0),P(x,y),M(![]() ,0),若實數λ使向量
,0),若實數λ使向量![]() ,λ
,λ![]() ,
,![]() 滿足λ2·(
滿足λ2·(![]() )2=
)2=![]() ·
·![]() 。
。
(1)求點P的軌跡方程,并判斷P點的軌跡是怎樣的曲線;
(2)當λ=![]() 時,過點A1且斜率為1的直線與此時(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使ΔA1BC為正三角形(請說明理由)。
時,過點A1且斜率為1的直線與此時(1)中的曲線相交的另一點為B,能否在直線x=-9上找一點C,使ΔA1BC為正三角形(請說明理由)。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧沈陽二中等重點中學協作體高三領航高考預測(二)文數學卷(解析版) 題型:解答題
(本題滿分12分)在 中
中 分別為A,B,C所對的邊,
分別為A,B,C所對的邊, 且
且
(1)判斷 的形狀;
的形狀;
(2)若
 ,求
,求 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源:2013屆云南大理州賓川四中高二下學期4月考試文科數學試卷(解析版) 題型:解答題
(本題滿分12分)在各項為正的數列 中,數列的前n項和
中,數列的前n項和 滿足
滿足

(1)求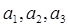 ;(2) 由(1)猜想數列
;(2) 由(1)猜想數列 的通項公式;(3) 求
的通項公式;(3) 求
查看答案和解析>>
科目:高中數學 來源:2013屆云南省高二上學期期末考試理科數學 題型:解答題
(本題滿分12分)在邊長為2的正方體 中,E是BC的中點,F是
中,E是BC的中點,F是 的中點
的中點
(Ⅰ)求證:CF∥平面
(Ⅱ)求二面角 的平面角的余弦值。
的平面角的余弦值。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com