
 如圖,已知直角梯形ABCD所在的平面垂直于平面ABE,∠EAB=∠ABC=90°,∠DAB=60°,AB=AD=AE,P為線段BE的中點.
如圖,已知直角梯形ABCD所在的平面垂直于平面ABE,∠EAB=∠ABC=90°,∠DAB=60°,AB=AD=AE,P為線段BE的中點.分析 (Ⅰ)取AE的中點F,連接DF、PF,由已知證得PF∥DC,且PF=DC,則四邊形DCPF為平行四邊形,可得PC∥DF.再由線面平行的判定可得CP∥平面DAE;
(II)由∠BAE=90°,平面ABCD平面ABE,在平面ABCD內過A作Az⊥AB.以點A為原點,直線AE為x軸,直線AB為y軸,Az為z軸建立空間直角坐標系A-xyz,
設AB=AD=AE=2,求得E,C,D的坐標,進一步求出平面ECD與平面平面ABC的一個法向量,由兩法向量所成角的余弦值可得平面CDE與平面ABE所成的銳二面角θ的余弦值;
(Ⅲ)設Q(x,y,z),且$\overrightarrow{EQ}=λ\overrightarrow{EC}$,由向量相等求得Q(2-2λ,2λ,$\sqrt{3}λ$),又P(1,1,0),可得$\overrightarrow{PQ}=(1-2λ,2λ-1,\sqrt{3}λ)$.結合直線PQ與平面CDE所成的角的正弦值為$\frac{3\sqrt{6}}{14}$列式求得$λ=\frac{2}{9}$或$λ=\frac{2}{33}$.
解答 (Ⅰ)證明:取AE的中點F,連接DF、PF,
∵P為BE中點,∴PF∥AB,且PF=$\frac{1}{2}AB$,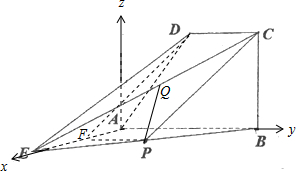
又直角梯形ABCD中,∠DAB=60°,AB=AD,
可得DC∥AB,且DC=$\frac{1}{2}AB$,
∴PF∥DC,且PF=DC,則四邊形DCPF為平行四邊形,可得PC∥DF.
而DF?平面EAD,PC?平面EAD,∴CP∥平面DAE;
(II)解:∵∠BAE=90°,平面ABCD平面ABE,在平面ABCD內過A作Az⊥AB.
∴以點A為原點,直線AE為x軸,直線AB為y軸,Az為z軸建立空間直角坐標系A-xyz,
設AB=AD=AE=2,由已知,得E(2,0,0),C(0,2,$\sqrt{3}$),D(0,1,$\sqrt{3}$).
∴$\overrightarrow{EC}=(-2,2,\sqrt{3})$,$\overrightarrow{DC}=(0,1,0)$,
設平面ECD的法向量為$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=-2x+2y+\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{DC}=y=0}\end{array}\right.$,取z=2,得平面ECD的一個法向量為$\overrightarrow{n}$=($\sqrt{3}$,0,2).
又∵平面ABC的一個法向量為$\overrightarrow{m}$=(0,0,1).
∴cosθ=|cos<$\overrightarrow{m},\overrightarrow{n}$>|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{2}{\sqrt{7}}=\frac{2\sqrt{7}}{7}$,
即平面CDE與平面ABE所成的銳二面角θ的余弦值為$\frac{2\sqrt{7}}{7}$;
(Ⅲ)解:線段EC上存在點Q,使直線PQ與平面CDE所成的角的正弦值為$\frac{3\sqrt{6}}{14}$,此時$\frac{EQ}{EC}$=$\frac{2}{9}$或$\frac{EQ}{EC}$=$\frac{2}{33}$.
設Q(x,y,z),且$\overrightarrow{EQ}=λ\overrightarrow{EC}$,則(x-2,y,z)=(-2$λ,2λ,\sqrt{3λ}$),
∴$\left\{\begin{array}{l}{x-2=-2λ}\\{y=2λ}\\{z=\sqrt{3}λ}\end{array}\right.$,即Q(2-2λ,2λ,$\sqrt{3}λ$),P(1,1,0),
則$\overrightarrow{PQ}=(1-2λ,2λ-1,\sqrt{3}λ)$.
∵直線PQ與平面CDE所成的角的正弦值為$\frac{3\sqrt{6}}{14}$,
∴|cos<$\overrightarrow{PQ},\overrightarrow{n}$>|=|$\frac{\overrightarrow{PQ}•\overrightarrow{n}}{|\overrightarrow{PQ}||\overrightarrow{n}|}$|=$\frac{|\sqrt{3}(1-2λ)+2\sqrt{3}λ|}{\sqrt{2(1-2λ)^{2}+3{λ}^{2}}•\sqrt{7}}=\frac{3\sqrt{6}}{14}$.
解得:$λ=\frac{2}{9}$或$λ=\frac{2}{33}$.
∴$\frac{EQ}{EC}$=$\frac{2}{9}$或$\frac{EQ}{EC}$=$\frac{2}{33}$.
點評 本題考查線面平行的判定,考查空間想象能力和思維能力,訓練了利用空間向量求線面角與面面角,是中檔題.


科目:高中數學 來源: 題型:選擇題
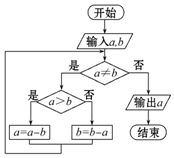 某同學根據“更相減損術”設計出程序框圖(圖).若輸入a的值為98,b的值為63,則執行該程序框圖輸出的結果為( )
某同學根據“更相減損術”設計出程序框圖(圖).若輸入a的值為98,b的值為63,則執行該程序框圖輸出的結果為( )| A. | 0 | B. | 7 | C. | 14 | D. | 21 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在某小學體育素質達標運動會上,對10名男生和10名女生在一分鐘跳繩的次數進行統計,得到如下所示莖葉圖:
在某小學體育素質達標運動會上,對10名男生和10名女生在一分鐘跳繩的次數進行統計,得到如下所示莖葉圖:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
| 平均氣溫(℃) | 33 | 30 | 32 | 30 | 25 |
| 用電量(萬度) | 38 | 35 | 41 | 36 | 30 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{π}^{3}}{81}$+$\frac{1}{2}$ | B. | $\frac{{π}^{3}}{81}$-$\frac{1}{2}$ | C. | $\frac{2π}{3}$-$\frac{1}{2}$ | D. | $\frac{2π}{3}$+$\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com