已知冪函數(shù)y=x m2-2m-2(m∈Z)的圖象與x軸、y軸都無(wú)公共點(diǎn)且是偶函數(shù),求m的值,并畫(huà)出函數(shù)的圖象(要求列表)
分析:根據(jù)冪函數(shù)的定義和性質(zhì)確定m的值,然后作出對(duì)應(yīng)的冪函數(shù)的圖象.
解答:解:∵冪函數(shù)y=x
m2-2m-2(m∈Z)的圖象、y軸都無(wú)公共點(diǎn),
∴m
2-2m-2<0,
即1-
<m<1+,
∵m∈Z,
∴m=0,1,2.
若m=0,則y=x
-2=為偶函數(shù),滿足條件.
若m=1,則y=x
-3=
為奇函數(shù),不滿足條件,舍去.
若m=2,則y=x
-2=為偶函數(shù),滿足條件.
∴m=0或m=2,冪級(jí)數(shù)y=x
-2=為偶函數(shù).
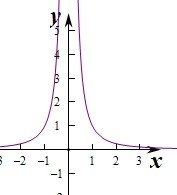
列表,取值描點(diǎn)得冪函數(shù)的圖象為:
| x |
-2 |
-1 |
- |
|
1 |
2 |
3 |
| y |
|
1 |
4 |
4 |
1 |
|
|
點(diǎn)評(píng):本題主要考查冪函數(shù)的圖象和性質(zhì),要求熟練掌握冪函數(shù)的定義和性質(zhì),注意要對(duì)m進(jìn)行分類討論.




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
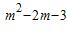 (m∈Z)的圖象與x軸y軸都無(wú)公共點(diǎn),且關(guān)于y軸對(duì)稱,則實(shí)數(shù)m的值是( )
(m∈Z)的圖象與x軸y軸都無(wú)公共點(diǎn),且關(guān)于y軸對(duì)稱,則實(shí)數(shù)m的值是( )