
【題目】已知函數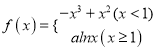
求![]() 在區間
在區間![]() 上的極小值和極大值點。
上的極小值和極大值點。
求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1) ![]() ,
, ![]() 極小值0,
極小值0, ![]() 為極大值點.(2)當
為極大值點.(2)當![]() 時,最大值
時,最大值![]() ,當
,當![]() 時,最大值為2.
時,最大值為2.
【解析】試題分析:(1)當![]() 時,求導函數,確定函數的單調性,可得
時,求導函數,確定函數的單調性,可得![]() 在區間
在區間![]() 上的極小值和極大值點;(2)分兩種情況
上的極小值和極大值點;(2)分兩種情況![]() ,
, ![]() 討論,分別利用導數確定函數的單調性,即可得到
討論,分別利用導數確定函數的單調性,即可得到![]() 在
在![]() 上的極大值,與區間端點值的函數值比較即可的結果.
上的極大值,與區間端點值的函數值比較即可的結果.
試題解析:(1)當![]() 時,
時, ![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,當
,當![]() 變化時,
變化時, ![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 極小值 | 極大值 |
![]() 當
當![]() 時,函數
時,函數![]() 取得極小值,
取得極小值, ![]() ,函數
,函數![]() 取得極大值點為
取得極大值點為![]() .
.
(2)①當![]() 時,
時, ![]() ,由(1)知,函數
,由(1)知,函數![]() 在
在![]() 和
和![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
②當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() ,綜上所述,當
,綜上所述,當![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() ;當
;當![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求證:
,求證: ![]() ⊥
⊥ ![]() ;
;
(2)設c=(0,1),若 ![]() +
+ ![]() =c,求α,β的值.
=c,求α,β的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)的最小值為1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在區間[2a,a+1]上不單調,求實數a的取值范圍;
(3)在區間[﹣1,1]上,y=f(x)的圖象恒在y=2x+2m+1的圖象上方,試確定實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax2-lnx。
(Ⅰ)當a=![]() 時,判斷f(x)的單調性;(Ⅱ)設f(x)≤x3+4x-lnx,在定義域內恒成立,求a的取值范圍。
時,判斷f(x)的單調性;(Ⅱ)設f(x)≤x3+4x-lnx,在定義域內恒成立,求a的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 兩城相距
兩城相距![]() ,在兩城之間距
,在兩城之間距![]() 城
城![]() 處建一核電站給
處建一核電站給![]() 兩城供電,為保證城市安全,核電站距城市距離不得小于
兩城供電,為保證城市安全,核電站距城市距離不得小于![]() .已知供電費用等于供電距離
.已知供電費用等于供電距離![]() 的平方與供電量(億度)之積的
的平方與供電量(億度)之積的![]() 倍,若
倍,若![]() 城供電量為每月20億度,城供電量為每月10億度.
城供電量為每月20億度,城供電量為每月10億度.
(1)把月供電總費用![]() 表示成
表示成![]() 的函數;
的函數;
(2)核電站建在距![]() 城多遠,才能使供電總費用
城多遠,才能使供電總費用![]() 最少?
最少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司研發出一款新產品,批量生產前先同時在甲、乙兩城市銷售30天進行市場調查.調查結果發現:甲城市的日銷售量![]() 與天數
與天數![]() 的對應關系服從圖①所示的函數關系;乙城市的日銷售量
的對應關系服從圖①所示的函數關系;乙城市的日銷售量![]() 與天數
與天數![]() 的對應關系服從圖②所示的函數關系;每件產品的銷售利潤
的對應關系服從圖②所示的函數關系;每件產品的銷售利潤![]() 與天數
與天數![]() 的對應關系服從圖③所示的函數關系,圖①是拋物線的一部分.
的對應關系服從圖③所示的函數關系,圖①是拋物線的一部分.
圖① ,圖②
,圖② ,圖③
,圖③
(1)設該產品的銷售時間為![]() ,日銷售利潤為
,日銷售利潤為![]() ,求
,求![]() 的解析式;
的解析式;
(2)若在30天的銷售中,日銷售利潤至少有一天超過2萬元,則可以投入批量生產,該產品是否可以投入批量生產,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 函數f(x)=x3+(m﹣4)x2﹣3mx+(n﹣6)x∈R的圖象關于原點對稱,其中m,n為實常數.
(1)求m,n的值;
(2)試用單調性的定義證明:f(x)在區間[﹣2,2]上是單調函數;
(3)當﹣2≤x≤2 時,不等式f(x)≥(n﹣logma)logma恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com