
【題目】已知數列![]() 滿足對任意的
滿足對任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列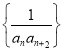 的前
的前![]() 項和為
項和為![]() ,不等式
,不等式![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:
(1)當n=1,n=2時,直接代入條件![]() 且
且![]() ,可求得;
,可求得;
(2)遞推一項,然后做差得![]() ,所以
,所以![]() ;由于
;由于![]() ,即當
,即當![]() 時都有
時都有![]() ,所以數列
,所以數列![]() 是首項為1,公差為1的等差數列,故求得數列
是首項為1,公差為1的等差數列,故求得數列![]() 的通項公式;
的通項公式;
(3)由(2)知![]() ,則
,則![]() ,利用裂項相消法得
,利用裂項相消法得![]() ,根據
,根據![]() 單調遞增得
單調遞增得![]() ,要使不等式
,要使不等式![]() 對任意正整數n恒成立,只要
對任意正整數n恒成立,只要![]() ,即可求得實數a的取值范圍.
,即可求得實數a的取值范圍.
試題解析:
(1)解:當![]() 時,有
時,有![]() ,
,
由于![]() ,所以
,所以![]() .
.
當![]() 時,有
時,有![]() ,
,
將![]() 代入上式,由于
代入上式,由于![]() ,所以
,所以![]() .
.
(2)解:由于![]() ,①
,①
則有![]() .②
.②
②-①,得![]() ,
,
由于![]() ,所以
,所以![]() ③
③
同樣有![]() ,④
,④
③-④,得![]() .
.
所以![]() .
.
由于![]() ,即當
,即當![]() 時都有
時都有![]() ,
,
所以數列![]() 是首項為1,公差為1的等差數列.
是首項為1,公差為1的等差數列.
故![]() .
.
(3)解:由(2)知![]() ,則
,則![]() ,所以
,所以
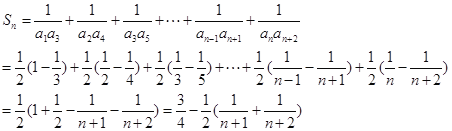
![]() ,∴數列
,∴數列![]() 單調遞增 .
單調遞增 .
![]() .
.
要使不等式![]() 對任意正整數n恒成立,只要
對任意正整數n恒成立,只要![]() .
.
![]() .
.
![]() ,即
,即![]() .
.
所以,實數a的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數 ![]()
(1)判斷f(x)的奇偶性并證明;
(2)若f(x)的定義域為[α,β](β>α>0),判斷f(x)在定義域上的增減性,并加以證明;
(3)若0<m<1,使f(x)的值域為[logmm(β﹣1),logmm(α﹣1)]的定義域區間[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某公司的職工食堂中,食堂每天以3元/個的價格從面包店購進面包,然后以5元/個的價格出售.如果當天賣不完,剩下的面包以1元/個的價格賣給飼料加工廠.根據以往統計資料,得到食堂每天面包需求量的頻率分布直方圖如圖所示.食堂某天購進了 90個面包,以![]() (個)(其中
(個)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利潤.
(元)表示利潤.
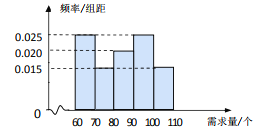
(1)根據直方圖計算需求量的中位數;
(2)估計利潤![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方圖的需求量分組中,以需求量落入該區間的頻率作為需求量在該區間的概率,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)與y軸的交點為A,B(點A位于點B的上方),F為左焦點,原點O到直線FA的距離為
=1(a>b>0)與y軸的交點為A,B(點A位于點B的上方),F為左焦點,原點O到直線FA的距離為 ![]() b.
b.
(1)求橢圓C的離心率;
(2)設b=2,直線y=kx+4與橢圓C交于不同的兩點M,N,求證:直線BM與直線AN的交點G在定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…)
(n=2,3,4,…)
(1)求a3、a4的值;
(2)設bn= ![]() (n∈N*),試用bn表示bn+1并求{bn} 的通項公式;
(n∈N*),試用bn表示bn+1并求{bn} 的通項公式;
(3)設cn= ![]() (n∈N*),求數列{cn}的前n項和Sn .
(n∈N*),求數列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某聯歡晚會舉行抽獎活動,舉辦方設置了甲、乙兩種抽獎方案,方案甲的中獎率為 ![]() ,中獎可以獲得2分;方案乙的中獎率為P0(0<P0<1),中獎可以獲得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中獎與否互不影響,晚會結束后憑分數兌換獎品. (Ⅰ)張三選擇方案甲抽獎,李四選擇方案乙抽獎,記他們的累計得分為X,若X≤3的概率為
,中獎可以獲得2分;方案乙的中獎率為P0(0<P0<1),中獎可以獲得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中獎與否互不影響,晚會結束后憑分數兌換獎品. (Ⅰ)張三選擇方案甲抽獎,李四選擇方案乙抽獎,記他們的累計得分為X,若X≤3的概率為 ![]() ,求P0;
,求P0;
(Ⅱ)若張三、李四兩人都選擇方案甲或都選擇方案乙進行抽獎,問:他們選擇何種方案抽獎,累計得分的數學期望較大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 的部分圖象如圖所示,則下列結論錯誤的是( )
的部分圖象如圖所示,則下列結論錯誤的是( ) 
A.![]()
B.函數f(x)在 ![]() 上單調遞增
上單調遞增
C.函數f(x)的一條對稱軸是 ![]()
D.為了得到函數f(x)的圖象,只需將函數y=2cosx的圖象向右平移 ![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=sin(x﹣ ![]() )的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得圖象向左平移
)的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得圖象向左平移 ![]() 個單位,則所得函數圖象對應的解析式為( )
個單位,則所得函數圖象對應的解析式為( )
A.y=sin( ![]() x﹣
x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin ![]() x
x
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com