
【題目】已知橢圓C的中心在原點,一個焦點F(﹣2,0),且長軸長與短軸長的比是 ![]() .
.
(1)求橢圓C的方程;
(2)設點M(m,0)在橢圓C的長軸上,點P是橢圓上任意一點.當 ![]() 最小時,點P恰好落在橢圓的右頂點,求實數m的取值范圍.
最小時,點P恰好落在橢圓的右頂點,求實數m的取值范圍.
【答案】
(1)解:設橢圓C的方程為 ![]() .
.
由題意 
解得a2=16,b2=12.
所以橢圓C的方程為 ![]()
(2)解:設P(x,y)為橢圓上的動點,由于橢圓方程為 ![]() ,故﹣4≤x≤4.
,故﹣4≤x≤4.
因為 ![]() ,
,
所以  =
= ![]() .
.
因為當 ![]() 最小時,點P恰好落在橢圓的右頂點,
最小時,點P恰好落在橢圓的右頂點,
即當x=4m時, ![]() 取得最小值.而x∈[﹣4,4],
取得最小值.而x∈[﹣4,4],
故有4m≥4,解得m≥1.
又點M在橢圓的長軸上,即﹣4≤m≤4.
故實數m的取值范圍是m∈[1,4].
【解析】(Ⅰ)設橢圓C的標準方程,根據焦點坐標和長軸長與短軸長的比聯立方程求得a和b,進而可得橢圓的方程.(Ⅱ)設P(x,y)為橢圓上的動點,根據橢圓的性質可判斷x的范圍.代入 ![]() 判斷因為當
判斷因為當 ![]() 最小時,點P恰好落在橢圓的右頂點,
最小時,點P恰好落在橢圓的右頂點,
進而求得m的范圍.點M在橢圓的長軸上進而推脫m的最大和最小值.綜合可得m的范圍.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 是定義在
是定義在 ![]() 上的奇函數,且
上的奇函數,且  偶函數
偶函數 ![]() 的定義域為
的定義域為 ![]() ,且當
,且當 ![]() 時,
時, ![]() .若存在實數
.若存在實數 ![]() ,使得
,使得 ![]() 成立,則實數
成立,則實數 ![]() 的取值范圍是( )
的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知一艘海監船O上配有雷達,其監測范圍是半徑為25 km的圓形區域,一艘外籍輪船從位于海監船正東40 km的A處出發,徑直駛向位于海監船正北30 km的B處島嶼,速度為28 km/h.
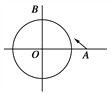
問:這艘外籍輪船能否被海監船監測到?若能,持續時間多長?(要求用坐標法)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x2﹣2ax﹣8a2(a>0),記不等式f(x)≤0的解集為A.
(1)當a=1時,求集合A;
(2)若(﹣1,1)A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() )x2+2bx在區間[3,5]上不是單調函數,則函數f(x)在R上的極大值為( )
)x2+2bx在區間[3,5]上不是單調函數,則函數f(x)在R上的極大值為( )
A.![]() b2﹣
b2﹣ ![]() b3
b3
B.![]() b﹣
b﹣ ![]()
C.0
D.2b﹣ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2﹣(2a+1)x+lnx(a∈R) (Ⅰ)當a>0時,求函數f(x)的單調區間;
(Ⅱ)設g(x)=f(x)+2ax,若g(x)有兩個極值點x1 , x2 , 且不等式g(x1)+g(x2)<λ(x1+x2)恒成立,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年存節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過600 元(含600元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種. 方案一:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,一次性摸出3個球,其中獎規則為:若摸到3個紅球,享受免單優惠;若摸到2個紅球,則打6折;若摸到1個紅球,則打7折;若沒摸到紅球,則不打折.
方案二:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,有放回每次摸取1球,連摸3次,每摸到1次紅球,立減200元.
(1)若兩個顧客均分別消費了 600元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
(2)若某顧客消費恰好滿1000元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com