
設橢圓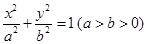 的左右頂點分別為
的左右頂點分別為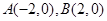 ,離心率
,離心率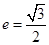 .過該橢圓上任一點
.過該橢圓上任一點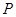 作
作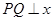 軸,垂足為
軸,垂足為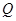 ,點
,點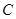 在
在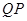 的延長線上,且
的延長線上,且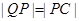 .
.
(1)求橢圓的方程;
(2)求動點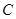 的軌跡
的軌跡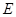 的方程;
的方程;
(3)設直線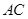 (
(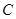 點不同于
點不同于 )與直線
)與直線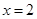 交于點
交于點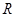 ,
,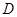 為線段
為線段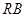 的中點,試判斷直線
的中點,試判斷直線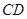 與曲線
與曲線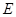 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
(1)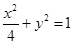 ;(2)
;(2)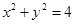 ;(3)詳見解析.
;(3)詳見解析.
【解析】
試題分析:(1)根據橢圓的幾何性質求出橢圓標準方程中的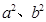 ;(2)用設點、建立兩個動點之間坐標的關系和代入已知曲線方程的方法求出動點軌跡方程;(3)先利用
;(2)用設點、建立兩個動點之間坐標的關系和代入已知曲線方程的方法求出動點軌跡方程;(3)先利用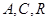 三點共線建立
三點共線建立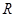 與
與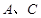 的坐標關系,再根據
的坐標關系,再根據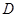 為線段
為線段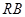 的中點求出
的中點求出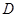 的坐標表達式,進一步求出直線
的坐標表達式,進一步求出直線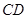 的方程,最后根據曲線
的方程,最后根據曲線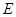 圓心到直線
圓心到直線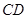 的距離與半徑的大小情況判斷其位置關系.
的距離與半徑的大小情況判斷其位置關系.
試題解析:(1)由題意可得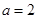 ,
, ,∴
,∴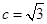 ,
2分
,
2分
∴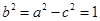 ,所以橢圓的方程為
,所以橢圓的方程為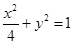 . 4分
. 4分
(2)設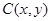 ,
, ,由題意得
,由題意得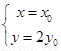 ,即
,即 ,
6分
,
6分
又 ,代入得
,代入得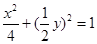 ,即
,即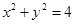 .
.
即動點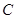 的軌跡
的軌跡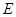 的方程為
的方程為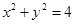 . 8分
. 8分
(3)設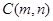 ,點
,點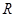 的坐標為
的坐標為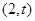 ,∵
,∵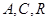 三點共線,∴
三點共線,∴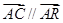 ,
,
而 ,
,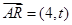 ,則
,則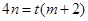 ,∴
,∴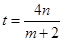 ,
,
∴點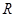 的坐標為
的坐標為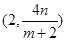 ,點
,點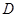 的坐標為
的坐標為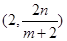 ,
10分
,
10分
∴直線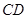 的斜率為
的斜率為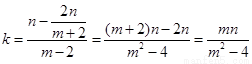 ,
,
而 ,∴
,∴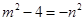 ,∴
,∴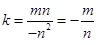 ,
12分
,
12分
∴直線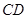 的方程為
的方程為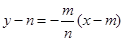 ,化簡得
,化簡得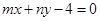 ,
,
∴圓心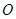 到直線
到直線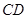 的距離
的距離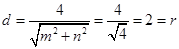 ,
,
所以直線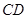 與圓
與圓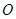 相切. 14分
相切. 14分
考點:1、橢圓的標準方程,2、代入法求動點軌跡方程,3、直線與圓位置關系的判定問題.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源:2013-2014學年河南省南陽市高三第三次聯考(高考模擬)理科數學試卷(解析版) 題型:解答題
已知圓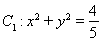 ,直線
,直線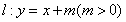 與圓
與圓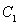 相切,且交橢圓
相切,且交橢圓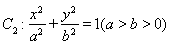 于
于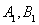 兩點,c是橢圓的半焦距,
兩點,c是橢圓的半焦距,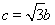
(1)求m的值;
(2)O為坐標原點,若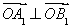 ,求橢圓
,求橢圓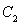 的方程;
的方程;
(3)在(2)的條件下,設橢圓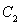 的左右頂點分別為A,B,動點
的左右頂點分別為A,B,動點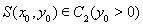 ,直線
,直線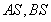 與直線
與直線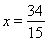 分別交于M,N兩點,求線段MN的長度的最小值
分別交于M,N兩點,求線段MN的長度的最小值
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河南省南陽市高三第三次聯考(高考模擬)文科數學試卷(解析版) 題型:解答題
已知圓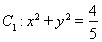 ,直線
,直線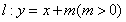 與圓
與圓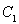 相切,且交橢圓
相切,且交橢圓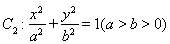 于
于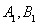 兩點,c是橢圓的半焦距,
兩點,c是橢圓的半焦距,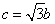 .
.
(1)求m的值;
(2)O為坐標原點,若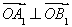 ,求橢圓
,求橢圓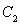 的方程;
的方程;
(3)在(2)的條件下,設橢圓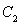 的左右頂點分別為A,B,動點
的左右頂點分別為A,B,動點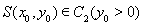 ,直線
,直線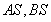 與直線
與直線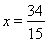 分別交于M,N兩點,求線段MN的長度的最小值.
分別交于M,N兩點,求線段MN的長度的最小值.
查看答案和解析>>
科目:高中數學 來源:2015屆廣東肇慶高二上學期期末質量檢測理科數學卷(解析版) 題型:解答題
設橢圓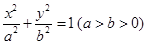 的左右頂點分別為
的左右頂點分別為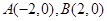 ,離心率
,離心率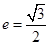 .過該橢圓上任一點P作PQ⊥x軸,垂足為Q,點C在QP的延長線上,且
.過該橢圓上任一點P作PQ⊥x軸,垂足為Q,點C在QP的延長線上,且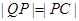 .
.
(1)求橢圓的方程;
(2)求動點C的軌跡E的方程;
(3)設直線AC(C點不同于A,B)與直線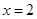 交于點R,D為線段RB的中點,試判斷直線CD與曲線E的位置關系,并證明你的結論.
交于點R,D為線段RB的中點,試判斷直線CD與曲線E的位置關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西南昌市高三第二次模擬測試文科數學試卷(解析版) 題型:解答題
已知橢圓C: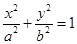 的離心率等于
的離心率等于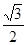 ,點P
,點P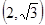 在橢圓上。
在橢圓上。
(1)求橢圓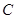 的方程;
的方程;
(2)設橢圓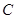 的左右頂點分別為
的左右頂點分別為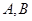 ,過點
,過點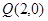 的動直線
的動直線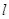 與橢圓
與橢圓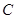 相交于
相交于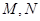 兩點,是否存在定直線
兩點,是否存在定直線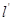 :
: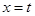 ,使得
,使得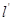 與
與 的交點
的交點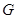 總在直線
總在直線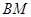 上?若存在,求出一個滿足條件的
上?若存在,求出一個滿足條件的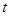 值;若不存在,說明理由.
值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山西省高三下學期5月月考理科數學試卷(解析版) 題型:解答題
已知橢圓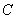 :
: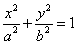 的離心率等于
的離心率等于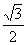 ,點
,點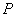
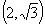 在橢圓上.
在橢圓上.
(I)求橢圓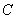 的方程;
的方程;
(Ⅱ)設橢圓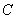 的左右頂點分別為
的左右頂點分別為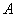 ,
,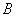 ,過點
,過點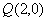 的動直線
的動直線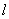 與橢圓
與橢圓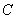 相交于
相交于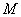 ,
,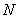 兩點,是否存在定直線
兩點,是否存在定直線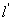 :
: ,使得
,使得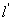 與
與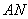 的交點
的交點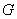 總在直線
總在直線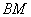 上?若存在,求出一個滿足條件的
上?若存在,求出一個滿足條件的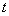 值;若不存在,說明理由。
值;若不存在,說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com