
【題目】已知函數![]() .(
.(![]() )
)
(Ⅰ)討論![]() 的單調性;
的單調性;
(Ⅱ)若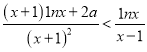 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】【試題分析】(1)運用導數與函數單調性之間的關系進行分析求解;(2)先將不等式進行等價轉化再運用導數知識與分類整合思想分析求解:
解:(Ⅰ)定義域是![]() ,
, ![]()
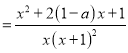 .
.
令![]() .
.
當![]() ,即
,即![]() 時,
時, ![]() 恒成立,即
恒成立,即![]() ,所以
,所以![]() 的單調增區間為
的單調增區間為![]() ;
;
當![]() 時,即
時,即![]() 或
或![]() 時,方程
時,方程![]() 有兩個不等的實根,
有兩個不等的實根,
![]() ,
, ![]() .
.
若![]() ,由
,由![]() ,
, ![]() 得,
得, ![]() ,所以
,所以![]() 在
在![]() 成立,
成立,
即![]() ,所以
,所以![]() 的單調增區間為
的單調增區間為![]() ;
;
若![]() ,由
,由![]() ,
, ![]() 得,
得, ![]() ,
,
由![]() 得
得![]() 的范圍是
的范圍是![]() ,由
,由![]() 得
得![]() 的范圍
的范圍![]() ,
,
即![]() 的單調遞增區間為
的單調遞增區間為![]() ,
, ![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
綜上所述,當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為
![]() ,
, ![]() ,
,
![]() 的單調遞減區間為
的單調遞減區間為![]() ;
;
當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為![]() ,無遞減區間.
,無遞減區間.
(Ⅱ)由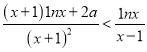 ,得
,得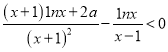 ,
,
即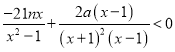 ,即
,即![]() ,即
,即![]() .
.
由(Ⅰ)可知當![]() 時,
時, ![]() 的單調遞增區間為
的單調遞增區間為![]() ,又
,又![]() ,
,
所以當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ;
;
又當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ;
;
所以![]() ,即原不等式成立.
,即原不等式成立.
由(Ⅰ)可知當![]() 時,
時, ![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,
單調遞減,
且![]() ,得
,得![]() ,
, ![]() ,
,
而![]() ,所以
,所以![]() 與條件矛盾.
與條件矛盾.
綜上所述, ![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖所示的一塊木料中,棱BC平行于面A′C′.
(Ⅰ)要經過面A′C′內的一點P和棱BC將木料鋸開,應怎樣畫線?
(Ⅱ)所畫的線與平面AC是什么位置關系?并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了讓學生了解環保知識,增強環保意識,某中學舉行了一次“環保知識競賽”,共有800名學生參加了這次競賽.為了解本次競賽成績情況,從中抽取了部分學生的成績進行統計. 請你根據尚未完成并有局部污損的頻率分布表和頻率分布直方圖,解答下列問題:
分組 | 頻數 | 頻率 |
50.5~60.5 | 6 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 15 | |
80.5~90.5 | 24 | 0.32 |
90.5~100.5 | ||
合計 | 75 | 1.00 |
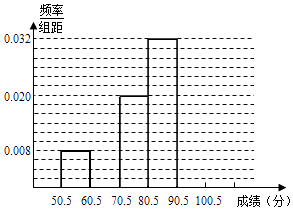
(1)填充頻率分布表的空格;
(2)補全頻率分布直方圖;
(3)根據頻率分布直方圖求此次“環保知識競賽”的平均分為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,側面
的正方形,側面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:面![]() 平面
平面![]() ;
;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一組數據的平均數是2.8,方差是3.6,若將這組數據中的每一個數據都加上60,得到一組新數據,則所得新數據的平均數和方差分別是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高職院校進行自主招生文化素質考試,考試內容為語文、數學、英語三科,總分為200分.現從上線的考生中隨機抽取20人,將其成績用莖葉圖記錄如下:
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
(Ⅰ)計算上線考生中抽取的男生成績的方差![]() ;(結果精確到小數點后一位)
;(結果精確到小數點后一位)
(Ⅱ)從上述莖葉圖180分以上的考生中任選2人作為考生代表出席座談會,求所選考生恰為一男一女的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】六個面都是平行四邊形的四棱柱稱為平行六面體.已知在平行四邊形ABCD中(如圖1),有AC2+BD2=2(AB2+AD2),則在平行六面體ABCD﹣A1B1C1D1中(如圖2),AC12+BD12+CA12+DB12等于( ) 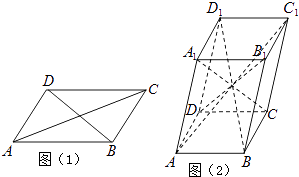
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com