
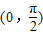 上單調(diào)遞增的是( )
上單調(diào)遞增的是( )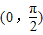 上的單調(diào)性,求出它們的周期,即可判斷選項.
上的單調(diào)性,求出它們的周期,即可判斷選項.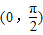 上是增函數(shù),不滿足題意;
上是增函數(shù),不滿足題意;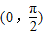 上是減函數(shù),不滿足題意;
上是減函數(shù),不滿足題意;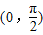 是增函數(shù),滿足題意;
是增函數(shù),滿足題意;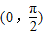 上不是增函數(shù);
上不是增函數(shù);

 初中學業(yè)考試導與練系列答案
初中學業(yè)考試導與練系列答案湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com