
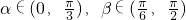 ,且α,β滿足
,且α,β滿足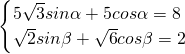
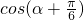 的值.
的值. sinα+5cosα=8,
sinα+5cosα=8, sinα+
sinα+ cosα)=8,即sin(α+
cosα)=8,即sin(α+ )=
)= ,(3分)
,(3分) ),∴α+
),∴α+ ∈(
∈( ,
, ),
), )=
)=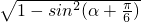 =
= ;(4分)
;(4分) sinβ+
sinβ+ cosβ=2,
cosβ=2, (
( sinβ+
sinβ+ cosβ)=2,即sin(β+
cosβ)=2,即sin(β+ )=
)= ,(6分)
,(6分) ,
, ),∴β+
),∴β+ ∈(
∈( ,
, ),
), )=-
)=- ,(7分)
,(7分) +(α+β)]=sin[(α+
+(α+β)]=sin[(α+ )+(β+
)+(β+ )]
)] )cos(β+
)cos(β+ )+cos(α+
)+cos(α+ )sin(β+
)sin(β+ )
) ×(-
×(- )+
)+ ×
× =-
=- .(12分)
.(12分) sinα+5cosα=8左邊提取10,利用兩角和與差的正弦函數公式及特殊角的三角函數值求出sin(α+
sinα+5cosα=8左邊提取10,利用兩角和與差的正弦函數公式及特殊角的三角函數值求出sin(α+ )的值,由α的范圍求出α+
)的值,由α的范圍求出α+ 的范圍,利用同角三角函數間的基本關系化簡即可求出cos(α+
的范圍,利用同角三角函數間的基本關系化簡即可求出cos(α+ )的值;
)的值; sinβ+
sinβ+ cosβ=2左邊提取2
cosβ=2左邊提取2 ,利用兩角和與差的正弦函數公式及特殊角的三角函數值化簡,求出sin(β+
,利用兩角和與差的正弦函數公式及特殊角的三角函數值化簡,求出sin(β+ )的值,由β的范圍求出β+
)的值,由β的范圍求出β+ 的范圍,利用同角三角函數間的基本關系求出cos(β+
的范圍,利用同角三角函數間的基本關系求出cos(β+ )的值,將所求式子利用誘導公式sin(
)的值,將所求式子利用誘導公式sin( +θ)=cosθ變形,其中的角
+θ)=cosθ變形,其中的角 +α+β變形為(α+
+α+β變形為(α+ )+(β+
)+(β+ ),利用兩角和與差的正弦函數公式化簡后,將各自的值代入即可求出值.
),利用兩角和與差的正弦函數公式化簡后,將各自的值代入即可求出值.

 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
| 7 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com