
【題目】紅外線治療儀的治療作用是在紅外線照射下,組織溫度升高,毛細血管擴張,血流加快,物質代謝增強,組織細胞活力及再生能力提高,對我們身體某些疾病的治療有著很大的貢獻,某藥店兼營某種紅外線治療儀,經過近![]() 個月的營銷,對銷售狀況進行相關數據分析,發現月銷售量與銷售價格有關,其統計數據如下表:
個月的營銷,對銷售狀況進行相關數據分析,發現月銷售量與銷售價格有關,其統計數據如下表:
每臺紅外線治療儀的銷售價格: |
|
|
|
|
|
紅外線治療儀的月銷售量: |
|
|
|
|
|
(1)根據表中數據求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)①每臺紅外線治療儀的價格為![]() 元時,預測紅外線治療儀的月銷售量;(四舍五入為整數)
元時,預測紅外線治療儀的月銷售量;(四舍五入為整數)
②若該紅外線治療儀的成本為![]() 元/臺,藥店為使每月獲得最大的純收益,利用(1)中結論,問每臺該種紅外線治療儀的銷售價格應定為多少元?(四舍五入,精確到
元/臺,藥店為使每月獲得最大的純收益,利用(1)中結論,問每臺該種紅外線治療儀的銷售價格應定為多少元?(四舍五入,精確到![]() 元).
元).
參考公式:回歸直線方程![]() ,
,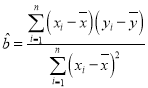 ,
,![]() .
.
【答案】(1)![]() ;(2)①紅外線治療儀的月銷量為
;(2)①紅外線治療儀的月銷量為![]() 臺;②價格應定為
臺;②價格應定為![]() 元.
元.
【解析】
(1)計算出![]() 、
、![]() 的值,將表格中的數據代入最小二乘法公式,求得
的值,將表格中的數據代入最小二乘法公式,求得![]() 和
和![]() 的值,即可得出
的值,即可得出![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)①將![]() 代入回歸直線方程,求得
代入回歸直線方程,求得![]() 的值,即可得出紅外線治療儀的月銷售量的預測值;
的值,即可得出紅外線治療儀的月銷售量的預測值;
②計算出藥店每月獲取得純利![]() 的函數解析式,利用二次函數的基本性質可求得
的函數解析式,利用二次函數的基本性質可求得![]() 取最大值時對應的
取最大值時對應的![]() 值,即可得解.
值,即可得解.
(1)![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() .
.
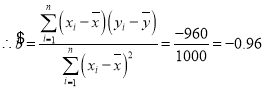 ,
,![]() ,
,
![]() 關于
關于![]() 的回歸方程為
的回歸方程為![]() ;
;
(2)①由(1)知,當![]() 時,
時,![]() ,
,
答:每臺紅外線治療儀的價格為![]() 元時,紅外線治療儀的月銷量為
元時,紅外線治療儀的月銷量為![]() 臺;
臺;
②藥店每月獲取得純利![]() .
.
所以當![]() 時,
時,![]() 取得最大值.
取得最大值.
答:藥店為使每月獲得最大的純收益,每臺該種紅外線治療儀的銷售價格應定為![]() 元.
元.


科目:高中數學 來源: 題型:
【題目】2015年12月10日,我國科學家屠呦呦教授由于在發現青蒿素和治療瘧疾的療法上的貢獻獲得諾貝爾醫學獎,以青蒿素類藥物為主的聯合療法已經成為世界衛生組織推薦的抗瘧疾標準療法,目前,國內青蒿人工種植發展迅速,調查表明,人工種植的青蒿的長勢與海撥高度、土壤酸堿度、空氣濕度的指標有極強的相關性,現將這三項的指標分別記為![]() ,并對它們進行量化:0表示不合格,1表示臨界合格,2表示合格,再用綜合指標
,并對它們進行量化:0表示不合格,1表示臨界合格,2表示合格,再用綜合指標![]() 的值評定人工種植的青蒿的長勢等級,若
的值評定人工種植的青蒿的長勢等級,若![]() ,則長勢為一級;若
,則長勢為一級;若![]() ,則長勢為二極;若
,則長勢為二極;若![]() ,則長勢為三級,為了了解目前人工種植的青蒿的長勢情況,研究人員隨機抽取了10塊青蒿人工種植地,得到如下結果:
,則長勢為三級,為了了解目前人工種植的青蒿的長勢情況,研究人員隨機抽取了10塊青蒿人工種植地,得到如下結果:
種植地編號 |
|
|
|
|
|
|
|
|
|
|
|
種植地編號 |
|
|
|
|
|
|
|
|
|
|
|
(1)若該地有青蒿人工種植地180個,試估計該地中長勢等級為三級的個數;
(2)從長勢等級為一級的青蒿人工種植地中隨機抽取兩個,求這兩個人工種植地的綜合指標![]() 均為4個概率.
均為4個概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (0<φ<π,ω>0)為偶函數,且函數y=f(x)圖象的兩相鄰對稱軸間的距離為
(0<φ<π,ω>0)為偶函數,且函數y=f(x)圖象的兩相鄰對稱軸間的距離為![]() .若將函數y=f(x)的圖象向右平移
.若將函數y=f(x)的圖象向右平移![]() 個單位后,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,則g(x)在下列區間上是減函數的是( )
個單位后,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,則g(x)在下列區間上是減函數的是( )
A. ![]() B. [0,π]
B. [0,π]
C. [2π,3π] D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|ax2+2x+1=0,a∈R},
(1)若A只有一個元素,試求a的值,并求出這個元素;
(2)若A是空集,求a的取值范圍;
(3)若A中至多有一個元素,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖像相鄰對稱軸之間的距離是
的圖像相鄰對稱軸之間的距離是![]() ,若將
,若將![]() 的圖像向右移
的圖像向右移![]() 個單位,所得函數
個單位,所得函數![]() 為奇函數.
為奇函數.
(1)求![]() 的解析式;
的解析式;
(2)若函數![]() 的零點為
的零點為![]() ,求
,求![]() ;
;
(3)若對任意![]() ,
,![]() 有解,求
有解,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年5月27日當今世界圍棋排名第一的柯潔在與![]() 的人機大戰中中盤棄子認輸,至此柯潔與
的人機大戰中中盤棄子認輸,至此柯潔與![]() 的三場比賽全部結束,柯潔三戰全負,這次人機大戰再次引發全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查,根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
的三場比賽全部結束,柯潔三戰全負,這次人機大戰再次引發全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查,根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
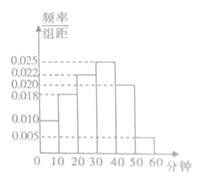
(1)請根據已知條件完成下面![]() 列聯表,并據此資料你是否有95%的把握認為“圍棋迷”與性別有關?
列聯表,并據此資料你是否有95%的把握認為“圍棋迷”與性別有關?
非圍棋迷 | 圍棋迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率,現在從該地區大量學生中,采用隨機抽樣方法每次抽取1名學生,抽取3次,記被抽取的3名學生中的“圍棋迷”人數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列,數學期望和方差.
的分布列,數學期望和方差.
獨立性檢查臨界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
(參考公式: 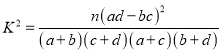 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
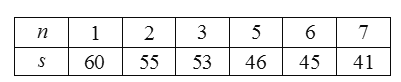
【題目】某農科所發現,一種作物的年收獲量![]() (單位:
(單位:![]() )與它“相近”作物的株數
)與它“相近”作物的株數![]() 具有相關關系(所謂兩株作物“相近”是指它們的直線距離不超過
具有相關關系(所謂兩株作物“相近”是指它們的直線距離不超過![]() ),并分別記錄了相近作物的株數為
),并分別記錄了相近作物的株數為![]() 時,該作物的年收獲量的相關數據如下:
時,該作物的年收獲量的相關數據如下:
(1)根據研究發現,該作物的年收獲量![]() 可能和它“相近”作物的株數
可能和它“相近”作物的株數![]() 有以下兩種回歸方程:
有以下兩種回歸方程:![]() ,利用統計知識,結合相關系數
,利用統計知識,結合相關系數![]() 比較使用哪種回歸方程更合適;
比較使用哪種回歸方程更合適;
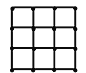
(2)農科所在如下圖所示的正方形地塊的每個格點(指縱、橫直線的交叉點)處都種了一株該作物,其中每個小正方形的面積為![]() ,若在所種作物中隨機選取一株,求它的年收獲量的分布列與數學期望.(注:年收獲量以(1)中選擇的回歸方程計算所得數據為依據)
,若在所種作物中隨機選取一株,求它的年收獲量的分布列與數學期望.(注:年收獲量以(1)中選擇的回歸方程計算所得數據為依據)
參考公式:線性回歸方程為![]() ,其中
,其中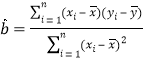 ,
,![]() ,
,
相關系數 ;
;
參考數值:![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,在
,在![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,四邊形
的中點,四邊形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() .
.

(Ⅰ)求異面直線![]() 與
與![]() 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸為極軸建立極坐標系,曲線
軸為極軸建立極坐標系,曲線![]() 的極坐標為
的極坐標為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 和曲線
和曲線![]() 有三個公共點,求以這三個公共點為頂點的三角形的面積.
有三個公共點,求以這三個公共點為頂點的三角形的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com