
【題目】數(shù)列{an}的前n項(xiàng)和是Sn , 且Sn+ ![]() =1.
=1.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)記bn=log3 ![]() ,數(shù)列
,數(shù)列 ![]() 的前n項(xiàng)和為Tn , 若不等式Tn<m,對任意的正整數(shù)n恒成立,求m的取值范圍.
的前n項(xiàng)和為Tn , 若不等式Tn<m,對任意的正整數(shù)n恒成立,求m的取值范圍.
【答案】
(1)解:由 ![]() ①
①
![]() ②
②
①﹣②可得 ![]() ,
,
∴ ![]() ,
,
當(dāng)n=1時 ![]() ,則
,則 ![]() ,
,
∴數(shù)列{an}是以 ![]() 為首項(xiàng),
為首項(xiàng), ![]() 為公比的等比數(shù)列,
為公比的等比數(shù)列,
因此 ![]()
(2)解: ![]() ,
,
∴ ![]() ,
, ![]() .
.
∵不等式Tn<m,對任意的正整數(shù)n恒成立,
∴ ![]()
【解析】(1)由 ![]() ,
, ![]() ,相減可得
,相減可得 ![]() ,再利用等比數(shù)列的通項(xiàng)公式即可得出;(2)利用對數(shù)的運(yùn)算性質(zhì)、“裂項(xiàng)求和”即可得出.
,再利用等比數(shù)列的通項(xiàng)公式即可得出;(2)利用對數(shù)的運(yùn)算性質(zhì)、“裂項(xiàng)求和”即可得出.
【考點(diǎn)精析】關(guān)于本題考查的數(shù)列的前n項(xiàng)和,需要了解數(shù)列{an}的前n項(xiàng)和sn與通項(xiàng)an的關(guān)系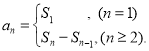 才能得出正確答案.
才能得出正確答案.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() :實(shí)數(shù)
:實(shí)數(shù)![]() 滿足
滿足![]() ,其中
,其中![]() ;
;![]() :實(shí)數(shù)
:實(shí)數(shù)![]() 滿足
滿足![]() .
.
(1)若![]() ,且
,且![]() 為真,
為真,![]() 為假,求實(shí)數(shù)
為假,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 是
是![]() 的充分不必要條件,求實(shí)數(shù)
的充分不必要條件,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 是定義域?yàn)?/span>
是定義域?yàn)?/span>![]() 的奇函數(shù).
的奇函數(shù).
(1)求![]() 的值.
的值.
(2)若![]() ,試求不等式
,試求不等式![]() 的解集;
的解集;
(3)若![]() 在
在![]() 上的最小值為
上的最小值為![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“雙十一”已經(jīng)成為網(wǎng)民們的網(wǎng)購狂歡節(jié),某電子商務(wù)平臺對某市的網(wǎng)民在今年“雙十一”的網(wǎng)購情況進(jìn)行摸底調(diào)查,用隨機(jī)抽樣的方法抽取了100人,其消費(fèi)金額![]() (百元)的頻率分布直方圖如圖所示:
(百元)的頻率分布直方圖如圖所示:

(1)求網(wǎng)民消費(fèi)金額![]() 的平均值和中位數(shù)
的平均值和中位數(shù)![]() ;
;
(2)把下表中空格里的數(shù)填上,能否有90%的把握認(rèn)為網(wǎng)購消費(fèi)與性別有關(guān);


查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,等比數(shù)列
,等比數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】試題分析:(1)設(shè)等差數(shù)列![]() 公差為
公差為![]() ,等比數(shù)列
,等比數(shù)列![]() 公比為
公比為![]() ,由已知條件求出
,由已知條件求出![]() ,再寫出通項(xiàng)公式;(2)由
,再寫出通項(xiàng)公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
試題解析:設(shè)等差數(shù)列![]() 公差為
公差為![]() ,等比數(shù)列
,等比數(shù)列![]() 公比為
公比為![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,結(jié)合
,結(jié)合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
當(dāng)![]() 時,
時,![]() ,此時
,此時![]() ;
;
當(dāng)![]() 時,
時,![]() ,此時
,此時![]() .
.
【題型】解答題
【結(jié)束】
20
【題目】如圖,已知直線與拋物線![]() 相交于
相交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,
, ![]() 交
交![]() 于
于![]() ,且點(diǎn)
,且點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
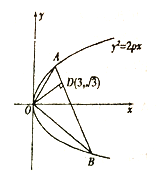
(1)求![]() 的值;
的值;
(2)若![]() 為拋物線的焦點(diǎn),
為拋物線的焦點(diǎn), ![]() 為拋物線上任一點(diǎn),求
為拋物線上任一點(diǎn),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有4個人去參加娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇.為增加趣味性,約定:每個人通過擲一枚質(zhì)地均勻的骰子決定自己去參加哪個游戲,擲出點(diǎn)數(shù)為1或2的人去參加甲游戲,擲出點(diǎn)數(shù)大于2的人去參加乙游戲.
(1)求這4個人中恰有2人去參加甲游戲的概率;
(2)求這4個人中去參加甲游戲的人數(shù)大于去參加乙游戲的人數(shù)的概率;
(3)用X,Y分別表示這4個人中去參加甲、乙游戲的人數(shù),記ξ=|X﹣Y|,求隨機(jī)變量ξ的分布列與數(shù)學(xué)期望Eξ.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當(dāng)![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關(guān)于![]() 的方程
的方程![]() 的解集中恰有一個元素,求
的解集中恰有一個元素,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,若對任意
,若對任意![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)= ![]() ,其中a>﹣1.若f(x)在R上是增函數(shù),則實(shí)數(shù)a的取值范圍是( )
,其中a>﹣1.若f(x)在R上是增函數(shù),則實(shí)數(shù)a的取值范圍是( )
A.[e+1,+∞)
B.(e+1,+∞)
C.(e﹣1,+∞)
D.[e﹣1,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量m=(cos![]() ,sin
,sin ![]() ),n=(2
),n=(2![]() +sinx,2
+sinx,2![]() -cos
-cos![]() ),函數(shù)
),函數(shù)![]() =m·n,x∈R.
=m·n,x∈R.
(1) 求函數(shù)![]() 的最大值;
的最大值;
(2) 若![]()
![]()
![]() 且
且 ![]() =1,求
=1,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com