
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)當![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上的最大值為
上的最大值為![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求實數(shù)b的取值范圍.
成立,求實數(shù)b的取值范圍.
【答案】(Ⅰ)![]() (Ⅱ)當
(Ⅱ)當![]() 時,遞增區(qū)間為
時,遞增區(qū)間為![]() ,
, ![]() ,遞減區(qū)間為
,遞減區(qū)間為![]()
當![]() 時,函數(shù)
時,函數(shù)![]() 的遞增區(qū)間為
的遞增區(qū)間為![]() ,遞減區(qū)間為
,遞減區(qū)間為![]()
【解析】(Ⅰ)當![]() 時,
時, ![]()
![]() ……………………1分
……………………1分
![]()
![]() …………………………………….…2分
…………………………………….…2分
所以曲線![]() 在點
在點![]() 處的切線方程
處的切線方程![]() …………………………….…3分
…………………………….…3分
(Ⅱ)![]() ………4分
………4分
當![]() 時,
時,
解![]() ,得
,得![]() ,解
,解![]() ,得
,得![]()
所以函數(shù)![]() 的遞增區(qū)間為
的遞增區(qū)間為![]() ,遞減區(qū)間為在
,遞減區(qū)間為在![]() ………………………5分
………………………5分
x |
|
|
|
|
| |||||
f’(x) | + | - | + | |||||||
f(x) | 增 | 減 | 增 | |||||||
![]() 時,令
時,令![]() 得
得![]() 或
或![]()
當![]() 時,
時, ![]()
函數(shù)![]() 的遞增區(qū)間為
的遞增區(qū)間為![]() ,
, ![]() ,遞減區(qū)間為
,遞減區(qū)間為![]() ……………………7分
……………………7分
當![]() 時,
時, ![]() 在
在![]() 上
上![]() ,在
,在![]() 上
上![]() 8分
8分
函數(shù)![]() 的遞增區(qū)間為
的遞增區(qū)間為![]() ,遞減區(qū)間為
,遞減區(qū)間為![]() ………………………9分
………………………9分
(Ⅲ)由(Ⅱ)知,當![]() 時,
時, ![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 上是減函數(shù),
上是減函數(shù),
所以![]() , ……………………………11分
, ……………………………11分
存在![]() ,使
,使![]() 即存在
即存在![]() ,使
,使![]() ,
,
方法一:只需函數(shù)![]() 在[1,2]上的最大值大于等于
在[1,2]上的最大值大于等于![]()
所以有 即
即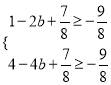 解得:
解得: ![]() …13分
…13分
方法二:將![]()
整理得![]()
![]() 從而有
從而有![]()
所以![]() 的取值范圍是
的取值范圍是![]() .………13分
.………13分


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了調(diào)查高一新生中女生的體重情況,校衛(wèi)生室隨機選20名女生作為樣本,測量她們的體重(單位:kg),獲得的所有數(shù)據(jù)按照區(qū)間![]() ,
, ![]() ,
, ![]() ,
, ![]() 進行分組,得到頻率分布直方圖如圖所示,已知樣本中體重在區(qū)間
進行分組,得到頻率分布直方圖如圖所示,已知樣本中體重在區(qū)間![]() 上的女生數(shù)與體重在區(qū)間
上的女生數(shù)與體重在區(qū)間![]() 上的女生數(shù)之比為
上的女生數(shù)之比為![]() .
.

(1)求![]() 的值;
的值;
(2)從樣本中體重在區(qū)間![]() 上的女生中隨機抽取兩人,求體重在區(qū)間
上的女生中隨機抽取兩人,求體重在區(qū)間![]() 上的女生至少有一人被抽中的概率.
上的女生至少有一人被抽中的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高中為了解高中學(xué)生的性別和喜愛打籃球是否有關(guān),對50名高中學(xué)生進行了問卷調(diào)查,得到如下列聯(lián)表:
喜愛打籃球 | 不喜歡打籃球 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 |
已知在這50人中隨機抽取1人,抽到喜歡打籃球的學(xué)生的概率為![]() .
.
(1)請將上述列聯(lián)表補充完整;
(2)判斷是否有99.5%的把握認為喜歡打籃球與性別有關(guān)?
附: 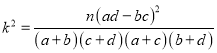
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為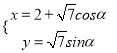 (其中
(其中![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() :
: ![]() ,以坐標原點
,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的極坐標方程;
的極坐標方程;
(2)若射線![]() (
(![]() )與曲線
)與曲線![]() ,
, ![]() 分別交于
分別交于![]() ,
, ![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 是定義在
是定義在![]() 上的偶函數(shù),
上的偶函數(shù), ![]() 為其導(dǎo)函數(shù),當
為其導(dǎo)函數(shù),當![]() 時,
時, ![]() ,且
,且![]() ,則不等式
,則不等式![]() 的解集為( )
的解集為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知袋中放有形狀大小相同的小球若干,其中標號為0的小球1個,標號為1的小球1個,標號為2的小球![]() 個,從袋中隨機抽取一個小球,取到標號為2的小球的概率為
個,從袋中隨機抽取一個小球,取到標號為2的小球的概率為![]() ,現(xiàn)從袋中不放回地隨機取出2個小球,記第一次取出的小球標號為
,現(xiàn)從袋中不放回地隨機取出2個小球,記第一次取出的小球標號為![]() ,第二次取出的小球標號為
,第二次取出的小球標號為![]() .
.
(1)記“![]() ”為事件
”為事件![]() ,求事件
,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
(2)在區(qū)間![]() 上任取兩個實數(shù)
上任取兩個實數(shù)![]() ,求事件
,求事件![]() “
“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在
在![]() 內(nèi)存在兩個極值點,求
內(nèi)存在兩個極值點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為豐富人民群眾業(yè)余生活,某市擬建設(shè)一座江濱公園,通過專家評審篩選處建設(shè)方案A和B向社會公開征集意見,有關(guān)部分用簡單隨機抽樣方法調(diào)查了500名市民對這兩種方案的看法,結(jié)果用條形圖表示如下:
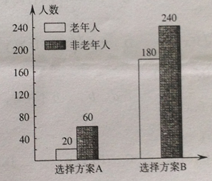
(1)根據(jù)已知條件完成下面![]() 列聯(lián)表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過
列聯(lián)表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過![]() 的前提下認為是否選擇方案A和年齡段有關(guān)?
的前提下認為是否選擇方案A和年齡段有關(guān)?
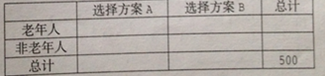
(2)根據(jù)(1)的結(jié)論,能否提出一個更高的調(diào)查方法,使得調(diào)查結(jié)果更具代表性,說明理由.
附:

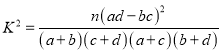
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com