【題目】如圖，幾何體
中，四邊形
為菱形，
，
，面
∥面，
、
、
都垂直于面，且
，
為
的中點，
為
的中點．
（1）求證：
為等腰直角三角形；
（2）求二面角
的余弦值．
【答案】(1)詳見解析;(2) 
.
【解析】
試題分析：（1）由已知條件，在直角三角形
，DCE中分別求出
，DE的長度，由邊的關(guān)系能夠證出△DB1E為等腰直角三角形；（2）取
的中點H，因為O，H分別為DB，
的中點，所以O(shè)H∥BB1，以O(shè)A，OB，OH分別為x，y，z軸建立坐標系，求出兩個平面
和DFE的法向量，根據(jù)二面角與其法向量所成角的關(guān)系求二面角
的余弦值．
試題解析：解：（1）連接
，交
于
，因為四邊形
為菱形，
，所以
因為
、
都垂直于面,
，又面
∥面,
所以四邊形
為平行四邊形 ,則
2分
因為、、
都垂直于面,則
4分
所以
所以
為等腰直角三角形 5分
（2）取
的中點
，因為
分別為
的中點，所以
∥
以
分別為
軸建立坐標系，
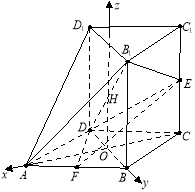
則
所以
7分
設(shè)面
的法向量為
，
則
，即
且
令
，則
9分
設(shè)面
的法向量為
則
即
且
令
，則
11分
則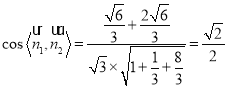
,則二面角
的余弦值為 12分
智能訓練練測考系列答案
計算高手系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，
，現(xiàn)有如下兩種圖象變換方案：
（方案1）：將函數(shù)
的圖象上所有點的橫坐標變?yōu)樵瓉淼囊话耄v坐標不變，再將所得圖象向左平移
個單位長度；
（方案2）：將函數(shù)的圖象向左平移
個單位長度，再將所得圖象上所有點的橫坐標變?yōu)樵瓉淼囊话耄v坐標不變.
請你從中選擇一種方案，確定在此方案下所得函數(shù)
的解析式，并解決如下問題：
（1）用“五點作圖法”畫出函數(shù)在
的閉區(qū)間上的圖象（列表并畫圖）；
（2）請你在答題紙相應位置逐一寫出函數(shù)的①周期性②奇偶性③單調(diào)遞增區(qū)間④單調(diào)遞減區(qū)間.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】定義區(qū)間
，
，
，
的長度均為
，多個區(qū)間并集的長度為各區(qū)間長度之和，例如, 
的長度
. 用
表示不超過
的最大整數(shù)，記
，其中
.設(shè)
，
，當
時,不等式
解集區(qū)間的長度為
，則
的值為
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
、
，離心率
，點
在橢圓
上.
（1）求橢圓
的方程；
（2）設(shè)過點
且不與坐標軸垂直的直線交橢圓
于
、
兩點，線段
的垂直平分線與
軸交于點
，求點
的橫坐標的取值范圍；
（3）在第（2）問的條件下，求
面積的最大值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知過坐標原點的直線l與圓C：x2+y2﹣8x+12＝0相交于不同的兩點A，B．
（1）求線段AB的中點P的軌跡M的方程．
（2）是否存在實數(shù)k，使得直線l1：y＝k（x﹣5）與曲線M有且僅有一個交點？若存在，求出k的取值范圍；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】(本小題滿分12分)已知橢圓
:
的焦距為
,離心率為
,其右焦點為
,過點
作直線交橢圓于另一點
．
（1）若
,求
外接圓的方程;
（2）若過點
的直線與橢圓
相交于兩點
、
，設(shè)
為
上一點，且滿足
（
為坐標原點），當
時，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】兩次購買同一種物品，可以用兩種不同的策略，第一種是不考慮物品價格的升降，每次購買這種物品的數(shù)量一定；第二種是不考慮物品價格的升降，每次購買這種物品所花的錢數(shù)一定.哪種購物方式比較經(jīng)濟？你能把所得結(jié)論作一些推廣嗎？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)函數(shù)
，曲線
在點
處的切線方程為
．
（1）求
，
的值；
（2）若
，求函數(shù)
的單調(diào)區(qū)間；
（3）設(shè)函數(shù)
，且
在區(qū)間
內(nèi)存在單調(diào)遞減區(qū)間，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
經(jīng)過點
，且離心率為
．
（Ⅰ）求橢圓
的方程；
（Ⅱ）設(shè)
是橢圓上的點，直線
與
（
為坐標原點）的斜率之積為
．若動點
滿足
，試探究是否存在兩個定點
，使得
為定值？若存在，求的坐標；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com