【答案】
分析:(1)設 θ
1<θ
2,θ
1、θ
2∈[0,
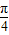
],根據三角函數的特點判斷f
1(θ
1)-f
1(θ
2)=(sinθ
1-sinθ
2)+(cosθ
2-cosθ
1)<0,從而得出結論;
(2)首先利用余弦的二倍角公式化簡原式的左邊等于cos
22θ,同理原式右邊也等于cos
22θ,從而證明結論.
(3)當n=1時,f
1(θ)在[0,
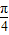
]上單調遞增,求出最值;當n=3時,f
3(θ)在[0,
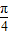
]上為單調遞增,求出最值;正奇數n≥5的情形,首先根據定義判斷出函數的單調遞增,從而得出f
n(θ)的最大值為f
n(
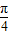
)=0,最小值為f
n(0)=-1.
解答:解:(1)f
1(θ)、f
3(θ)在0
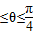
,上均為單調遞增的函數.
對于函數f
1(θ)=sinθ-cosθ,設 θ
1<θ
2,θ
1、θ
2∈[0,
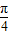
],則
f
1(θ
1)-f
1(θ
2)=(sinθ
1-sinθ
2)+(cosθ
2-cosθ
1),
∵sinθ
1<sinθ
2,cosθ
2<cosθ
1
∴f
1(θ
1)<f
1(θ
2)函數f
1(θ)在[0,
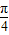
]上單調遞增.
(2)∵原式左邊=2(sin
6θ+cos
6θ)-(sin
4θ+cos
4θ)
=2(sin
2θ+cos
2θ)(sin
4θ-sin
2θcos
2θ+cos
4θ)-(sin
4θ+cos
4θ)
=1-sin
22θ=cos
22θ.
又∵原式右邊=(cos
2θ-sin
2θ)2=cos
22θ
∴2f
6(θ)-f
4(θ)=(cos
4θ-sin
4θ)(cos
2θ-sin
2θ).
(3)當n=1時,函數f
1(θ)在[0,
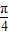
]上單調遞增,
∴
f1(θ)的最大值為f
1(
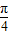
)=0,最小值為f
1(0)=-1.
當n=3時,函數f
3(θ)在[0,
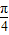
]上為單調遞增.
∴f
3(θ)的最大值為f
3(
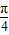
)=0,最小值為f
3(0)=-1.
下面討論正奇數n≥5的情形:對任意θ1、θ
2∈[0,
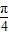
],且θ
1<θ
2
∵f
n(θ
1)-f
n(θ
2)=(sin
nθ
1-sin
nθ
2)+(cos
nθ
2-cos
nθ
1),
以及 0≤sinθ
1<sinθ
2<1 0≤cosθ
2<cosθ
1<1,
∴sin
nθ
1<sin
nθ
2 cos
nθ
2<cos
nθ
1,從而f
n(θ
1)<f
n(θ
2).
∴f
n(θ)在[0,
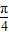
]上為單調遞增,
則f
n(θ)的最大值為f
n(
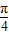
)=0,最小值為f
n(0)=-1.
綜上所述,當n為奇數時,函數f
n(θ)的最大值為0,最小值為-1.
點評:本題考查了三角函數的最值,函數單調性的判定以及同角三角函數的基本關系,一般根據定義判斷函數的單調性,此題有一定難度.

 ,其中n為正整數.
,其中n為正整數.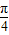 ],根據三角函數的特點判斷f1(θ1)-f1(θ2)=(sinθ1-sinθ2)+(cosθ2-cosθ1)<0,從而得出結論;
],根據三角函數的特點判斷f1(θ1)-f1(θ2)=(sinθ1-sinθ2)+(cosθ2-cosθ1)<0,從而得出結論;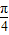 ]上單調遞增,求出最值;當n=3時,f3(θ)在[0,
]上單調遞增,求出最值;當n=3時,f3(θ)在[0,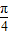 ]上為單調遞增,求出最值;正奇數n≥5的情形,首先根據定義判斷出函數的單調遞增,從而得出fn(θ)的最大值為fn(
]上為單調遞增,求出最值;正奇數n≥5的情形,首先根據定義判斷出函數的單調遞增,從而得出fn(θ)的最大值為fn(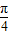 )=0,最小值為fn(0)=-1.
)=0,最小值為fn(0)=-1.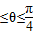 ,上均為單調遞增的函數.
,上均為單調遞增的函數.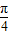 ],則
],則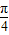 ]上單調遞增.
]上單調遞增.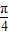 ]上單調遞增,
]上單調遞增,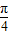 )=0,最小值為f1(0)=-1.
)=0,最小值為f1(0)=-1.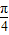 ]上為單調遞增.
]上為單調遞增.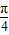 )=0,最小值為f3(0)=-1.
)=0,最小值為f3(0)=-1.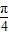 ],且θ1<θ2
],且θ1<θ2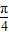 ]上為單調遞增,
]上為單調遞增,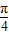 )=0,最小值為fn(0)=-1.
)=0,最小值為fn(0)=-1.

 如圖所示,矩形ABCD的邊長AB=6,BC=4,點F在DC上,DF=2.動點M、N分別從點D、B同時出發,沿射線DA、BA的方向運動,當第二次MF=MN時M、N兩點同時停止運動.連接FM、FN,當F、N、M不在同一直線時,可得△FMN,設動點M、N的速度都是1個單位/秒,M、N運動的時間為t秒.試解答下列問題:
如圖所示,矩形ABCD的邊長AB=6,BC=4,點F在DC上,DF=2.動點M、N分別從點D、B同時出發,沿射線DA、BA的方向運動,當第二次MF=MN時M、N兩點同時停止運動.連接FM、FN,當F、N、M不在同一直線時,可得△FMN,設動點M、N的速度都是1個單位/秒,M、N運動的時間為t秒.試解答下列問題: