
 時,直線l與圖象G恰有6個公共點;
時,直線l與圖象G恰有6個公共點;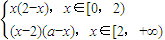 ,
,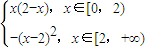 ,
, 時,x∈[0,+∞)時,f(x)=
時,x∈[0,+∞)時,f(x)=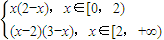 ,
, 可得x=
可得x=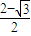 ,或x=
,或x= ,或x=
,或x= ,由函數圖象的對稱性可知,
,由函數圖象的對稱性可知,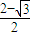 ,-
,- ,-
,- ,
,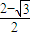 ,
, ,
, ,故②正確;
,故②正確;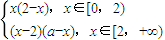 =m,
=m,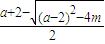 ,或x=
,或x=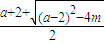 ,
, ,
,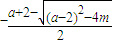 ,x3=
,x3=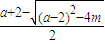 ,x4=
,x4= ,
,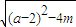 ,x3-x2=a+2-
,x3-x2=a+2-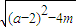 ,
,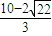 ,或a>
,或a>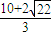 ,
,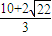 ,當然滿足a∈(4,+∞),使距離相等,
,當然滿足a∈(4,+∞),使距離相等,

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com